题目内容
已知曲线 的极坐标方程是
的极坐标方程是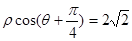 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: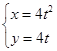 (
( 是参数).
是参数).
(1)将曲线 和曲线
和曲线 的方程转化为普通方程;
的方程转化为普通方程;
(2)若曲线 与曲线
与曲线 相交于
相交于 两点,求证
两点,求证 ;
;
(3)设直线 交于两点
交于两点 ,且
,且 (
( 且
且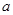 为常数),过弦
为常数),过弦 的中点
的中点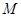 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线 于点
于点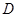 ,求证:
,求证: 的面积是定值.
的面积是定值.
 的极坐标方程是
的极坐标方程是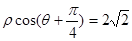 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: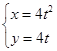 (
( 是参数).
是参数).(1)将曲线
 和曲线
和曲线 的方程转化为普通方程;
的方程转化为普通方程;(2)若曲线
 与曲线
与曲线 相交于
相交于 两点,求证
两点,求证 ;
;(3)设直线
 交于两点
交于两点 ,且
,且 (
( 且
且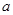 为常数),过弦
为常数),过弦 的中点
的中点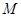 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线 于点
于点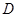 ,求证:
,求证: 的面积是定值.
的面积是定值.(1)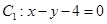 ;
;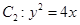 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.
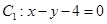 ;
;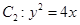 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.试题分析:(1)先将极坐标方程
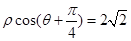 转化为
转化为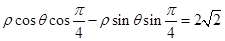 ,后由极坐标与普通方程转化的关系式
,后由极坐标与普通方程转化的关系式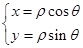 得出
得出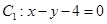 ;由
;由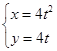 消去参数
消去参数 即可得到
即可得到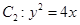 ;(2)联立方程
;(2)联立方程 消去
消去 得到
得到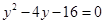 ,设
,设 ,根据根与系数的关系得到
,根据根与系数的关系得到 ,进而得到
,进而得到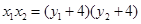 ,再检验
,再检验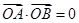 即可证明
即可证明 ;(3)联立方程
;(3)联立方程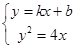 ,消
,消 得
得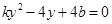 ,进而得到
,进而得到 ,由
,由 得出
得出 ,进而确定
,进而确定 的坐标,最后计算
的坐标,最后计算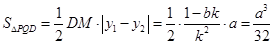 可得结论.
可得结论.(1)由极坐标方程
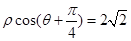 可得
可得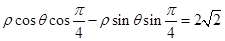
而
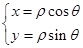 ,所以
,所以 即
即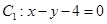
由
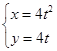 消去参数
消去参数 得到
得到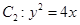
(2)设
 ,联立方程并消元得:
,联立方程并消元得: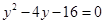
 ,
,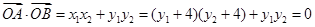

(3)
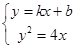 ,消
,消 得
得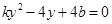 ,
,
由
 (
( 且
且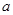 为常数),得
为常数),得
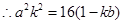 ,又可得
,又可得 中点
中点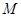 的坐标为
的坐标为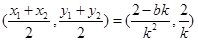
所以点
 ,
,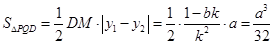 ,面积是定值.
,面积是定值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和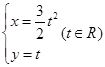 ,它们的交点坐标为____________.
,它们的交点坐标为____________. 为极点,
为极点, 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线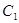 的极坐标方程为:
的极坐标方程为: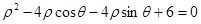 上的点到曲线
上的点到曲线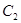 的参数方程为:
的参数方程为: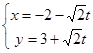 (
(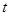 为参数)的距离的最小值为 .
为参数)的距离的最小值为 . (α为参数).
(α为参数).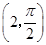 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;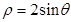 的圆心到极轴的距离为( )
的圆心到极轴的距离为( )
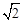
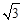
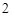
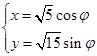 (
(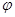 为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,点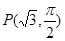 ,直线
,直线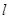 的极坐标方程为
的极坐标方程为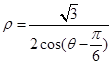 .
.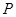 与直线l的位置关系,说明理由;
与直线l的位置关系,说明理由;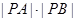 的值.
的值. 曲线C2的参数方程为
曲线C2的参数方程为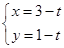 (
(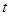 为参数),以极点为原点,极轴为
为参数),以极点为原点,极轴为 轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为
轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为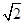
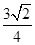
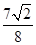
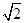 cosθ+sinθ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,求a的值.
cosθ+sinθ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,求a的值.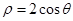 在点
在点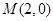 处的切线的极坐标方程为 .
处的切线的极坐标方程为 .