Question

直线y=-

3

3

x+m与圆x²+y²=1在第一象限内有两个不同的交点，则实数m取值范围是______．

Answer 1

分两种情况：当直线y=-

3

3

x+m过（0，1）时，将x=0，y=1代入得：m=1；
当直线y=-

3

3

x+m与圆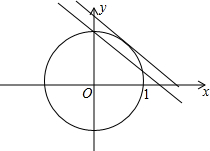x²+y²=1相切时，圆心到直线的距离d=r，即

|-m|

(- 3 3 )2+12

=1，
解得：m=

2 3

3

，
则直线与圆在第一象限内有两个不同的交点时，实数m的取值范围是（1，

2 3

3

）．
故答案为：（1，

2 3

3

）