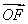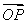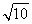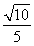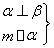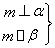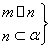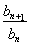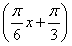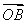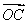题目内容
已知点集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)求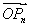 ·OPn+1的最小值;
·OPn+1的最小值;
(3)设cn=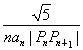 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.
(1)bn=2n-1(n∈N*).(2)3.(3)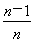
【解析】(1)由y=m·n,
m=(2x-2b,1), n=(1,1+2b),得y=2x+1,
即L的轨迹方程为y=2x+1.
∵P1为L的轨迹与y轴的交点,
∴P1(0,1),则a1=0,b1=1,
∵数列{an}为等差数列,且公差为1,
∴an=n-1(n∈N*),
代入y=2x+1,得bn=2n-1(n∈N*).
(2)∵Pn(n-1,2n-1),∴Pn+1(n,2n+1),
∴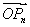 ·OPn+1=(n-1,2n-1)·(n,2n+1)
·OPn+1=(n-1,2n-1)·(n,2n+1)
=5n2-n-1=5 2-
2-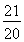 .
.
∵n∈N*,
∴当n=1时,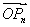 ·OPn+1有最小值,为3.
·OPn+1有最小值,为3.
(3)当n≥2时,由Pn(n-1,2n-1),
得an·|PnPn+1|=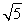 (n-1),
(n-1),
cn=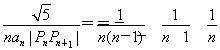 ,
,
∴c2+c3+…+cn=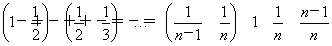

练习册系列答案
相关题目