题目内容
6．已知函数f（x）=$\left\{\begin{array}{l}{3{x}^{2}-4，x≥4}\\{0，x＜0}\end{array}\right.$，则f（f（1））=0．分析 由已知中函数f（x）=$\left\{\begin{array}{l}{3{x}^{2}-4，x≥4}\\{0，x＜0}\end{array}\right.$，将x=1代入可得：则f（f（1））值．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{3{x}^{2}-4，x≥4}\\{0，x＜0}\end{array}\right.$，
∴f（f（1））=f（-1）=0．
故答案为：0．
点评 本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题．
练习册系列答案
智能训练练测考系列答案
相关题目
16．设f（x）是定义在实数集R上的函数，且y=f（x+1）是偶函数，当x≥1时，f（x）=2x-1，则f（$\frac{2}{3}$），f（$\frac{3}{2}$），f（$\frac{1}{3}$）的大小关系是（ ）
| A． | f（$\frac{2}{3}$）＜f（$\frac{3}{2}$）＜f（$\frac{1}{3}$） | B． | f（$\frac{1}{3}$）＜f（$\frac{2}{3}$）＜f（$\frac{3}{2}$） | C． | f（$\frac{1}{3}$）＜f（$\frac{3}{2}$）＜f（$\frac{2}{3}$） | D． | f（$\frac{3}{2}$）＜f（$\frac{1}{3}$）＜f（$\frac{2}{3}$） |
17．函数f（x）在（-4，7）上是增函数，则使y=f（x-3）+2为增函数的区间为（ ）
| A． | （-2，3） | B． | （-1，7） | C． | （-1，10） | D． | （-10，-4） |
14．两条平行直线l1：3x-2y-1=0，l2：3x-2y+1=0的距离是（ ）
| A． | $\frac{{2\sqrt{13}}}{13}$ | B． | $\frac{{\sqrt{13}}}{13}$ | C． | $\frac{1}{13}$ | D． | $\frac{2}{13}$ |
18．
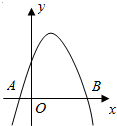如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）
如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）| A． | $\frac{c}{a}$ | B． | -$\frac{c}{a}$ | C． | ±$\frac{c}{a}$ | D． | -$\frac{a}{c}$ |
15．在复平面内，复数z=$\frac{2+i}{1-i}$，则其共轭复数z对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |