题目内容
1.已知点A(-3,5),B(2,15),直线l:3x-4y+4=0.(1)求过A点与直线l平行的直线方程;
(2)若P点在直线l上,求|PA|+|PB|的最小值.
分析 (1)设过A点与直线l平行的直线方程为3x-4y+m=0,把点A(-3,5)代入解得m即可得出.
(2)设点A关于直线l的对称点M(x,y),则$\left\{\begin{array}{l}{3×\frac{x-3}{2}-4×\frac{y+5}{2}+4=0}\\{\frac{y-5}{x+3}×\frac{3}{4}=-1}\end{array}\right.$,解得M.连接BM交直线l于点P,则点P即为所求.
解答 解:(1)设过A点与直线l平行的直线方程为3x-4y+m=0,把点A(-3,5)代入,可得-9-20+m=0,解得m=29.
∴过A点与直线l平行的直线方程为3x-4y+m=0.
(2)设点A关于直线l的对称点M(x,y),则$\left\{\begin{array}{l}{3×\frac{x-3}{2}-4×\frac{y+5}{2}+4=0}\\{\frac{y-5}{x+3}×\frac{3}{4}=-1}\end{array}\right.$,解得M(3,-3).
连接BM交直线l于点P,则点P即为所求.
∴|PA|+|PB|的最小值=|BM|=$\sqrt{(3-2)^{2}+(-3-15)^{2}}$=5$\sqrt{13}$.
点评 本题考查了线段的垂直平分线的性质、两点之间的距离公式、相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
11.函数f(x)=2cos(ωx+$\frac{π}{3}$)(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到函数g(x)=2sinωx的图象,只需将函数f(x)的图象( )
| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{5π}{12}$个单位长度 | D. | 向左平移$\frac{π}{3}$个单位长度 |
13.函数f(x)=$\frac{x}{1+x}\sqrt{\frac{1+x}{1-x}}$的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |
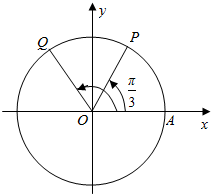 如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求:
如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求: