��Ŀ����
����Ŀ��2019��ij������һ������������ҵ�ƻ�����һ������Դ���������豸��ͨ���г�������ȫ����Ͷ��̶��ɱ�3000��Ԫ��ÿ����x��������������Ͷ��ɱ�![]() ��Ԫ����
��Ԫ���� �����г�����֪��ÿ�����ۼ�6��Ԫ����ȫ���������ij���������ȫ��������.
�����г�����֪��ÿ�����ۼ�6��Ԫ����ȫ���������ij���������ȫ��������.
��1�����2019�������![]() ����Ԫ�����������x���������ĺ�����ϵʽ��������=���۶�
����Ԫ�����������x���������ĺ�����ϵʽ��������=���۶�![]() �ɱ���
�ɱ���
��2��2019�����Ϊ���٣�������ʱ����ҵ���������������������.
���𰸡���1��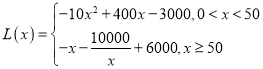 ����2��2019�������Ϊ100����ʱ����ҵ������������������Ϊ5800��Ԫ.
����2��2019�������Ϊ100����ʱ����ҵ������������������Ϊ5800��Ԫ.
��������
��1�����Ķ����⣬�ٷֵ�![]() ʱ����
ʱ����![]() ʱ����������ʽ���ɣ�
ʱ����������ʽ���ɣ�
��2����![]() ʱ�������䷽������κ��������ֵ����
ʱ�������䷽������κ��������ֵ����![]() ʱ�����þ�ֵ����ʽ���������ֵ��һ��Ҫע��ȡ�ȵ����������ۺ���ֶκ��������ֵ����.
ʱ�����þ�ֵ����ʽ���������ֵ��һ��Ҫע��ȡ�ȵ����������ۺ���ֶκ��������ֵ����.
�⣺��1������֪�е�![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]() ��
��
��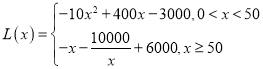 ��
��
��2����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ȡ���ֵ
ȡ���ֵ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
���ҽ���![]() ����
����![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
��![]()
��2019�������Ϊ100����ʱ����ҵ������������������Ϊ5800��Ԫ.

����Ŀ��2018��6��14�գ��ڶ�ʮһ�����籭�������ڶ���˹�������Ļ��ij��ѧ�ڶ��꼶�����ʾ�����,�Ӹ�У���꼶ѧ���г�ȡ��![]() �˽��е���,����Ů���ж������˶�����Ȥ��ռ
�˽��е���,����Ů���ж������˶�����Ȥ��ռ![]() ����������
����������![]() �˱�ʾ�������˶�û����Ȥ.
�˱�ʾ�������˶�û����Ȥ.
��1�����![]() ������,���ش��ܷ���
������,���ش��ܷ���![]() �İ�����Ϊ���������Ƿ�����Ȥ���Ա��йء���
�İ�����Ϊ���������Ƿ�����Ȥ���Ա��йء���
����Ȥ | û����Ȥ | �ϼ� | |
�� |
| ||
Ů | |||
�ϼ� |
��2������Ƶ����Ϊ����,���ٴӸ�У���꼶ȫ��ѧ����,������������ķ���ÿ����ȡ![]() ��ѧ��,��ȡ
��ѧ��,��ȡ![]() �Σ��DZ���ȡ��
�Σ��DZ���ȡ��![]() ��ѧ���ж���������Ȥ������Ϊ
��ѧ���ж���������Ȥ������Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
��:
|
|
|
|
|
|
|
|
|
|
![]()
����Ŀ��ij��ҵ��Ӧʡ�������٣��������豸���и��죬Ϊ�˷����豸����ǰ���Ч�����ִ��豸����ǰ�������Ĵ�����Ʒ�и���ȡ��![]() ����Ʒ��Ϊ���������һ������ָ��ֵ������������ָ��ֵ����
����Ʒ��Ϊ���������һ������ָ��ֵ������������ָ��ֵ����![]() �ڵIJ�Ʒ��Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.��ͼ���豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ����
�ڵIJ�Ʒ��Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.��ͼ���豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ����![]() ���豸������������Ƶ���ֲ���.
���豸������������Ƶ���ֲ���.
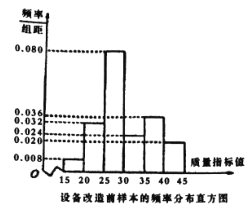
�����豸�����������Ƶ���ֲ���
����ָ��ֵ |
|
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
|
��1����������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
�İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
�豸����ǰ | �豸����� | �ϼ� | |
�ϸ�Ʒ | |||
���ϸ�Ʒ | |||
�ϼ� |
��2������Ƶ�ʷֲ�ֱ��ͼ�ͱ� �ṩ�����ݣ��ԴӲ�Ʒ�ϸ��ʵĽǶȶԸ���ǰ���豸�����ӽ��бȽϣ�
��3����ҵ�����ϸ�Ʒȫ�����ٺ��ݿͻ�����Ժϸ�Ʒ���еǼ�ϸ�֣�����ָ��ֵ����![]() �ڵĶ�Ϊһ��Ʒ��ÿ���ۼ�
�ڵĶ�Ϊһ��Ʒ��ÿ���ۼ�![]() Ԫ������ָ��ֵ����
Ԫ������ָ��ֵ����![]() ��
��![]() �ڵĶ�Ϊ����Ʒ��ÿ���ۼ�
�ڵĶ�Ϊ����Ʒ��ÿ���ۼ�![]() Ԫ�������ĺϸ�Ʒ��Ϊ����Ʒ��ÿ���ۼ�
Ԫ�������ĺϸ�Ʒ��Ϊ����Ʒ��ÿ���ۼ�![]() Ԫ.���ݱ�
Ԫ.���ݱ�![]() �����ݣ��ø���������һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е�Ƶ�ʴ�������в�Ʒ�г鵽һ����Ӧ�ȼ���Ʒ�ĸ���.����һ���˿��������������Ʒ������֧���ķ���Ϊ
�����ݣ��ø���������һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е�Ƶ�ʴ�������в�Ʒ�г鵽һ����Ӧ�ȼ���Ʒ�ĸ���.����һ���˿��������������Ʒ������֧���ķ���Ϊ![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����
|
|
|
|
|
|
|
|
|
|
|
|
![]()