题目内容
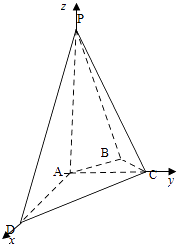
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 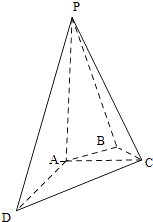
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
【答案】
(1)[解法一] 如图,以A为原点,建立空间直角坐标系,则A(0,0,0),D(2,0,0),C(0,1,0),B(﹣ ![]() ,
, ![]() ,0),P(0,0,2).
,0),P(0,0,2).
证明:易得 ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,0,0),于是
=(2,0,0),于是 ![]()
![]() =0,所以PC⊥AD.
=0,所以PC⊥AD.
[解法二] 证明:由PA⊥平面ABCD,可得PA⊥AD,
又由AD⊥AC,PA∩AC=A,故AD⊥平面PAC,
又PC平面PAC,
所以PC⊥AD.
(2)[解法一] 解: ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,﹣1,0),设平面PCD的一个法向量为
=(2,﹣1,0),设平面PCD的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 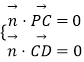 即
即 ![]()
取z=1,则以 ![]() =(1,2,1).又平面PAC的一个法向量为
=(1,2,1).又平面PAC的一个法向量为 ![]() =(1,0,0),于是cos<
=(1,0,0),于是cos< ![]() >=
>= ![]() =
= ![]() ,sin<
,sin< ![]() >=
>= ![]()
所以二面角A﹣PC﹣D的正弦值为 ![]()
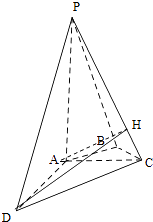
[解法二] 解:如图,作AH⊥PC于点H,连接DH,
由PC⊥AD,PC⊥AH,可得PC⊥平面ADH,因此DH⊥PC,从而∠AHD为二面角A﹣PC﹣D的平面角.
在RT△PAC中,PA=2,AC=1,所以AH= ![]() ,由(1)知,AD⊥AH,在RT△DAH中,DH=
,由(1)知,AD⊥AH,在RT△DAH中,DH= ![]() =
= ![]() ,因此sin∠AHD=
,因此sin∠AHD= ![]() =
= ![]() .所以二面角﹣PC﹣D的正弦值为
.所以二面角﹣PC﹣D的正弦值为 ![]()
(3)解法一:设E(0,0,h),其中h∈[0,2],由此得 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,h).由
,h).由 ![]() =(2,﹣1,0),故cos<
=(2,﹣1,0),故cos< ![]() >=
>= 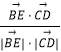 =
= 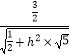 =
= ![]()
所以 ![]() =cos30°=
=cos30°= ![]() ,解得h=
,解得h= ![]() ,即AE=
,即AE= ![]() .
.
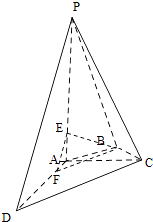
[解法二] 解:如图,因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,
设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.
由于BF∥CD,故∠AFB=∠ADC,在RT△DAC中,CD= ![]() ,sin∠ADC=
,sin∠ADC= ![]() ,故sin∠AFB=
,故sin∠AFB= ![]() .
.
在△AFB中,由 ![]() ,AB=
,AB= ![]() ,sin∠FAB=sin135°=
,sin∠FAB=sin135°= ![]() ,可得BF=
,可得BF= ![]() ,
,
由余弦定理,BF2=AB2+AF2﹣2ABAFcos∠FAB,得出AF= ![]() ,
,
设AE=h,在RT△EAF中,EF= ![]() =
= ![]() ,
,
在RT△BAE中,BE= ![]() =
= ![]() ,
,
在△EBF中,因为EF<BE,从而∠EBF=30°,
由余弦定理得到,cos30°= ![]() ,
,
解得h= ![]() ,
,
即AE= ![]() .
.
【解析】解法一(1)以A为原点,建立空间直角坐标系,通过得出 ![]()
![]() =0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos<
=0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos< ![]() >=cos30°=
>=cos30°= ![]() ,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
【考点精析】解答此题的关键在于理解用空间向量求直线间的夹角、距离的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则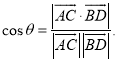 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 | 22 | b | 30 |
甲未参加 | c | 12 | d |
总计 | 30 | e | n |
(1)求b,c,d,e,n的值,据此能否有97.7%的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:0.2,0.5,0.2,0.1,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:0.4,0.2,0.6,0.2.则:
当他参加比赛时,求球队某场比赛输球的概率;
当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 7.879 | 10.828 |
![]() .
.
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度![]() 和对应的销售额
和对应的销售额![]() (万元)数据,如下表:
(万元)数据,如下表:
特产种类 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最满意度 |
|
|
|
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
|
|
|
![]() 求销量额
求销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() ;
;
![]() 我们约定:销量额
我们约定:销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() 的绝对值在
的绝对值在![]() 以上(含
以上(含![]() )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额![]() 关于最满意度
关于最满意度![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考数据:![]()
![]() ,
,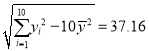 ,
,![]() ,
,![]() .
.
附:对于一组数据![]() .其回归直线方程
.其回归直线方程![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .线性相关系数
.线性相关系数

