题目内容
10．在等差数列{an}中，若a2=4，a4=2，则a6=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 6 |
分析 直接利用等差中项求解即可．
解答 解：在等差数列{an}中，若a2=4，a4=2，则a4=$\frac{1}{2}$（a2+a6）=$\frac{1}{2}（4+{a}_{6}）$=2，
解得a6=0．
故选：B．
点评 本题考查等差数列的性质，等差中项个数的应用，考查计算能力．
练习册系列答案
英才计划同步课时高效训练系列答案
相关题目
20．已知M（x0，y0）是双曲线C：$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点，F1，F2是C的左、右两个焦点，若$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$＜0，则y0的取值范围是（ ）
| A． | $（-\frac{\sqrt{3}}{3}，\frac{\sqrt{3}}{3}）$ | B． | $（-\frac{\sqrt{3}}{6}，\frac{\sqrt{3}}{6}）$ | C． | $（-\frac{2\sqrt{2}}{3}，\frac{2\sqrt{2}}{3}）$ | D． | $（-\frac{2\sqrt{3}}{3}，\frac{2\sqrt{3}}{3}）$ |
1．设变量x，y满足约束条件$\left\{\begin{array}{l}x+2≥0\\ x-y+3≥0\\ 2x+y-3≤0\end{array}\right.$，则目标函数z=x+6y的最大值为（ ）
| A． | 3 | B． | 4 | C． | 18 | D． | 40 |
18．
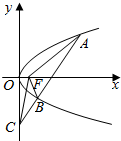如图，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在y轴上，则△BCF与△ACF的面积之比是（ ）
如图，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在y轴上，则△BCF与△ACF的面积之比是（ ）| A． | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B． | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C． | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D． | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
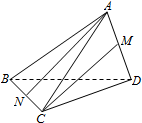如图，三棱锥A-BCD中，AB=AC=BD=CD=3，AD=BC=2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成的角的余弦值是$\frac{7}{8}$．
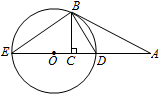如图，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C．