题目内容
已知下列命题中:
(1)若 ,且
,且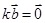 ,则
,则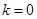 或
或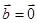 ,
,
(2)若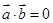 ,则
,则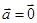 或
或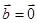
(3)若不平行的两个非零向量 ,满足
,满足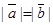 ,则
,则
(4)若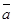 与
与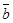 平行,则
平行,则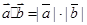 其中真命题的个数是( )
其中真命题的个数是( )
A. | B.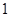 | C. | D.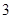 |
C
解析试题分析:对于(1)若 ,且
,且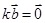 ,则
,则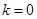 或
或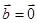 ,成立。
,成立。
对于(2)若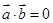 ,则
,则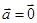 或
或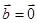 ,也可能是垂直的非零向量,错误。
,也可能是垂直的非零向量,错误。
对于(3)若不平行的两个非零向量 ,满足
,满足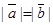 ,则
,则 ,成立。
,成立。
对于(4)若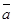 与
与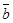 平行,则
平行,则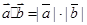 ,反向的时候不成立,错误。故选C.
,反向的时候不成立,错误。故选C.
考点:平面数量积的性质
点评:本题考查平面数量积的性质及运算律,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
“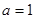 ”是“函数
”是“函数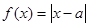 在区间
在区间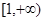 上为增函数”的( )
上为增函数”的( )
| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
已知 为实数,则“
为实数,则“ ”是“函数
”是“函数 在(0,1)上单调递增”的( )
在(0,1)上单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分且必要条件 | D.既不充分又不必要条件 |
若 则
则 是
是 成立的
成立的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知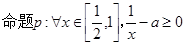 ;
; ,若
,若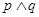 是真命题,则实数
是真命题,则实数 的取值范围为( )
的取值范围为( )
A.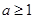 | B.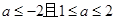 |
C.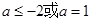 | D.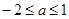 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
下列命题中,真命题是
A.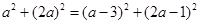 | B.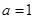 |
| C.a+b=0的充要条件是= -1 | D.a>1且b>1是ab>1的充分条件 |
如果a,b,c都是实数,那么P:ac<0,是q:关于x的方程ax2+bx+c=0有一个正根和一个负根的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于实数a,b,c,“a>b”是“ac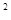 >bc
>bc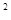 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |