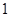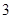题目内容
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
D
解析试题分析:线面平行的判定定理是说如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面相互平行,所以①不正确;根据面面垂直的判定定理知②不正确;垂直于同一条直线的两条直线不一定平行,也可能相交或异面,所以③不正确;根据面面垂直的判定定理知④正确.
考点:本小题主要考查空间直线、平面间的位置关系的判断和应用.
点评:解决此类问题,要紧扣相应的判定定理和性质定理,定理中的条件缺一不可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合 ,
, ,则“
,则“ ”是“
”是“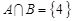 ”的 ( )
”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知x∈R,则x≥1是|x+1|+|x-1|=2|x|的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
已知命题 ,
, ,则
,则
A. , , | B. , , |
C. , , | D. , , |
下列命题中正确的是( )
A.函数 与 与 互为反函数 互为反函数 |
B.函数 与 与 都是增函数 都是增函数 |
C.函数 与 与 都是奇函数 都是奇函数 |
D.函数 与 与 都是周期函数 都是周期函数 |
给出以下四个说法:
①p或q为真命题是p且q为真命题的充分不必要条件;
②在刻画回归模型的拟合效果时,相关指数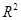 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量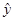 平均增加
平均增加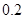 个单位;
个单位;
④对分类变量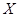 与
与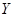 ,若它们的随机变量
,若它们的随机变量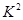 的观测值
的观测值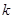 越小,则判断“
越小,则判断“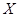 与
与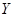 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是 ( )
| A.①④ | B.②④ | C.①③ | D.②③ |
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
| A.(-∞,1) | B.(-∞,2) | C.1 | D.2 |
命题“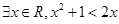 ”的否定为 ( )
”的否定为 ( )
A.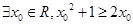 | B.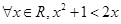 |
C.不存在实数x,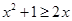 | D.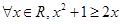 |
 ,且
,且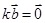 ,则
,则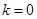 或
或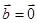 ,
,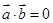 ,则
,则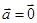 或
或 ,满足
,满足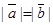 ,则
,则
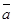 与
与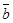 平行,则
平行,则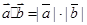 其中真命题的个数是( )
其中真命题的个数是( )