题目内容
7.设函数f(x)=|x+1|+|x-a|(1)若对于任意的实数x,不等式f(x)≥2恒成立,求实数a的取值范围;
(2)当a=2时,不等式f(x)≥k(x+1)+2恒成立,求实数k的取值范围.
分析 (1)根据绝对值的意义,|x+1|+|x-a|的最小值为|a+1|,由|a+1|≥2,求得实数a的取值范围;
(2)由题意可得f(x)的图象恒在直线y=ax的上方.再根据f(x)的表达式,画出图形,数形结合求得a的范围.
解答 解:(1)根据绝对值的意义,|x+1|+|x-a|表示数轴上的x对应点到-1、a对应点的距离之和,
它的最小值为|a+1|,
若不等式f(x)≥2对任意的实数x恒成立,则|a+1|≥2,求得a≥1,或a≤-3,
故实数a的取值范围为(-∞,-3]∪[1,+∞);
(2)由于不等式|x+1|+|x-2|≥k(x+1)+2恒成立,即f(x)的图象恒在直线y=k(x+1)+2的上方.
再根据f(x)=$\left\{\begin{array}{l}{-2x+1,x<-1}\\{3,-1≤x<2}\\{2x-1,x≥2}\end{array}\right.$,画出图形,如图: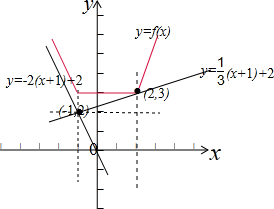
故直线y=k(x+1)+2的斜率k满足-2≤k≤$\frac{1}{3}$,
即a的范围为[-2,$\frac{1}{3}$].
点评 本题主要考查绝对值的意义,带由绝对值的函数,函数的恒成立问题,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
18.已知集合A={0,1,2,3},集合B={x|x2≤4},则A∩B=( )
| A. | {3} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
19.“0<a<2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,