桌面上有大小两颗球.相互靠在一起．已知大球的半径为9cm.小球半径4cm.则这两颗球分别与桌面相接触的两点之间的距离等于12 cm．题目和参考答案——青夏教育精英家教网——

题目内容

6．桌面上有大小两颗球，相互靠在一起．已知大球的半径为9cm，小球半径4cm，则这两颗球分别与桌面相接触的两点之间的距离等于12 cm．

分析由桌面上有大小两颗球，相互靠在一起，可知两圆相外切，由两颗球分别与桌面相接触的两点可知两圆与桌面相切，作出常用辅助线，构造出直角三角形，即可求出．

解答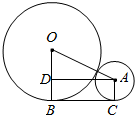解：由题意过两个球的球心与桌面垂直解得两个大圆可得：⊙O与⊙A相外切，两圆与桌面相切，切点为B，C，
连接OA，AC，OB，做AD⊥OB，
∴OA=9+4=13cm，OD=9-4=5cm，
∴AD=$\sqrt{{13}^{2}-{5}^{2}}$=12cm．
故答案为：12．

点评此题主要考查了球的解得性质的应用，取得截面问题，以及直线与圆相切的性质，结合实际问题是热点问题．考查空间想象能力以及计算能力．

练习册系列答案

王朝霞小升初重点校系列答案

专项卷和真题卷系列答案

文曲星中考总复习系列答案

问题引领系列答案

先锋题典系列答案

知识大集结系列答案

随堂口算系列答案

小学升学夺冠系列答案

培优好题系列答案

培优60课系列答案

相关题目

8．（Ⅰ）计算：$\frac{{8}^{\frac{2}{3}}×{3}^{lo{g}_{3}2}}{lne-lo{g}_{\frac{1}{64}}4}$；
（Ⅱ）化简：$\frac{sin（θ-π）•cos（\frac{π}{2}+θ）•cos（2017π-θ）}{sin（θ-\frac{π}{2}）•sin（θ+2016π）}$．

9．在等比数列{a_n}中，S_n是其前n项和，已知a₃=2S₂+1，a₄=2S₃+1，则S₄=（　　）

6．求函数y=$\frac{3x-1}{x+1}$（0≤x≤1）的最大值和最小值．

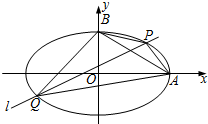已知平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点和上顶点分别为A，B，椭圆的离心率为$\frac{\sqrt{3}}{2}$，且过点（1，$\frac{\sqrt{3}}{2}$）．
（1）求椭圆的标准方程；
（2）如图，若直线l与该椭圆交于点P，Q两点，直线BQ，AP的斜率互为相反数．
①求证：直线l的斜率为定值；
②若点P在第一象限，设△ABP与△ABQ的面积分别为S₁，S₂，求$\frac{{S}_{1}}{{S}_{2}}$的最大值．

11．计算：
（1）（2$\frac{7}{9}$）${\;}^{\frac{1}{2}}$+（2$\frac{10}{27}$）${\;}^{-\frac{2}{3}}$-3π⁰+$\frac{37}{48}$
（2）lg0.001+ln$\sqrt{e}$+log₂（log₂16）+2${\;}^{-1+lo{g}_{2}3}$．

18．已知角α的顶点与原点O重合，始边与x轴的正半轴重合，若它的终边经过点P（2，3），则$tan（{2α+\frac{π}{4}}）$=（　　）

$-\frac{7}{17}$

$-\frac{12}{5}$

15．等差数列{a_n}中，若a₂，a₂₀₁₄为方程x²-10x+16=0的两根，则a₁+a₁₀₀₈+a₂₀₁₅=15．

16．设U=R，A={x|1≤x≤3}，B={x|2＜x≤4}，C={x|a≤x≤a+1}，a为实数，
（1）分别求A∩B，A∪（∁_UB）；
（2）若B∩C=C，求a的取值范围．