题目内容
15．等差数列{an}中，若a2，a2014为方程x2-10x+16=0的两根，则a1+a1008+a2015=15．分析 a2，a2014为方程x2-10x+16=0的两根，利用根与系数的关系可得：a2+a2014=10=2a1008，再利用等差数列的性质可得a1+a1008+a2015=3a1008，即可得出．
解答 解：∵a2，a2014为方程x2-10x+16=0的两根，
∴a2+a2014=10=2a1008，
解得a1008=5，
∵数列{an}是等差数列，
∴a1+a1008+a2015=3a1008=15．
故答案为：15．
点评 本题考查了一元二次方程的根与系数的关系、等差数列的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
3．
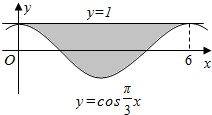已知图中阴影部分的面积为正整n，则二项式（x-$\frac{2}{\sqrt{x}}$）n 的展开式中的常数项为（ ）
已知图中阴影部分的面积为正整n，则二项式（x-$\frac{2}{\sqrt{x}}$）n 的展开式中的常数项为（ ）| A． | 240 | B． | 一240 | C． | 60 | D． | 一60 |
10．某校在对学生是否喜欢数学的抽样调查中，随机抽取了300名学生，相关的数据如表所示：
由表中数据直观分析，该校学生的性别与是否喜欢数学之间有关系（填“有”或“无”）．
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
20．设函数$f（x）=\left\{\begin{array}{l}2{x^2}-x，x≤0\\-{x^2}+2x，x＞0\end{array}\right.$，且关于x的方程f（x）=m，（m∈R）恰有3个不同的实数根x1，x2，x3，则x1x2x3的取值范围是（ ）
| A． | （-1，0） | B． | $（-\frac{1}{2}，+∞）$ | C． | （0，1） | D． | $（-\frac{1}{2}，0）$ |