题目内容
18.已知角α的顶点与原点O重合,始边与x轴的正半轴重合,若它的终边经过点P(2,3),则$tan({2α+\frac{π}{4}})$=( )| A. | $-\frac{7}{17}$ | B. | $\frac{17}{7}$ | C. | $-\frac{12}{5}$ | D. | $\frac{5}{12}$ |
分析 由条件利用任意角的三角函数的定义求得tanα,再利用二倍角的正切公式求得tan2α,再利用两角和的正切公式求得$tan({2α+\frac{π}{4}})$ 的值
解答 解:根据α的终边经过点P(2,3),可得tanα=$\frac{3}{2}$,tan2α=$\frac{2tanα}{1{-tan}^{2}α}$=-$\frac{12}{5}$,
∴$tan({2α+\frac{π}{4}})$=$\frac{tan2α+tan\frac{π}{4}}{1-tan2α•tan\frac{π}{4}}$=$\frac{-\frac{12}{5}+1}{1+\frac{12}{5}×1}$=-$\frac{7}{17}$,
故选:A.
点评 本题主要考查任意角的三角函数的定义,二倍角的正切公式、两角和的正切公式的应用,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.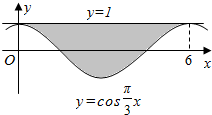 已知图中阴影部分的面积为正整n,则二项式(x-$\frac{2}{\sqrt{x}}$)n 的展开式中的常数项为( )
已知图中阴影部分的面积为正整n,则二项式(x-$\frac{2}{\sqrt{x}}$)n 的展开式中的常数项为( )
 已知图中阴影部分的面积为正整n,则二项式(x-$\frac{2}{\sqrt{x}}$)n 的展开式中的常数项为( )
已知图中阴影部分的面积为正整n,则二项式(x-$\frac{2}{\sqrt{x}}$)n 的展开式中的常数项为( )| A. | 240 | B. | 一240 | C. | 60 | D. | 一60 |
10.某校在对学生是否喜欢数学的抽样调查中,随机抽取了300名学生,相关的数据如表所示:
由表中数据直观分析,该校学生的性别与是否喜欢数学之间有关系(填“有”或“无”).
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
7.设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的 集合共有( ) 个.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.已知tanα=2,则sinαcosα=( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |