Question

【题目】在△ABC中，内角A，B，C的对边分别是a，b，c，已知c=6，sinA﹣sinC=sin（A﹣B）．若1≤a≤6，则sinC的取值范围是 ．

Answer 1

【答案】[ ，1]
【解析】解：∵sinA﹣sinC=sin（A﹣B）．
∴sinA=sin（A﹣B）+sinC=sin（A﹣B）+sin（A+B）=2sinAcosB，
∴由sinA≠0，可得：cosB= ，
∵c=6，
∴由余弦定理可得：b2=a2+c2﹣2accosB=a2﹣6a+36，
∴b= ，
于是由正弦定理可得sinC= = = ，
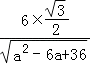∵1≤a≤6， ∈[3 ，6]，
从而得到sinC的取值范围是：[ ，1]．
所以答案是：[ ，1]．
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案，需要熟知正弦定理:．