题目内容
【题目】已知数列{an}是各项为正数的等比数列，且a2=9，a4=81．
（1）求数列{an}的通项公式an；
（2）若bn=log3an ， 求证：数列{bn}是等差数列．
【答案】
（1）解：设数列{an}的公比为q，∵a2=9，a4=81．
则 
，
又∵an＞0，∴q＞0，∴q=3，
故通项公式 
（2）证明：由（1）知 
，∴ 
，
∴bn+1﹣bn=（n+1）﹣n=1（常数），n∈N*，
故数列{bn}是一个公差等于1的等差数列
【解析】（1）利用等比数列的通项公式即可得出．（2）由（1）知 ，bn=n，只要证明bn+1﹣bn=（常数）即可得出．
【考点精析】利用等差关系的确定和数列的通项公式对题目进行判断即可得到答案，需要熟知如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
【题目】在某次测试后，一位老师从本班48同学中随机抽取6位同学，他们的语文、历史成绩如表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
（Ⅰ）若规定语文成绩不低于90分为优秀，历史成绩不低于80分为优秀，以频率作概率，分别估计该班语文、历史成绩优秀的人数；
（Ⅱ）用表中数据画出散点图易发现历史成绩
与语文成绩
具有较强的线性相关关系，求
与
的线性回归方程（系数精确到0.1）．
参考公式：回归直线方程是
，其中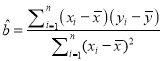
， 
