题目内容
1．设m、n、t为整数，集合{a|a=3m+3n+3t，0≤m＜n＜t}中的数由小到大组成数列{an}：13，31，37，39，…，则a21=733．分析 由题意列出部分m，n，t的取值，从而可得t=2时，${C}_{2}^{2}$=1，t=3时，${C}_{3}^{2}$=3，t=4时，${C}_{4}^{2}$=6，t=5时，${C}_{5}^{2}$=10；
故a21=30+31+36=733．
解答 解：由题意，数由小到大时m，n，t的取值如下，
0 1 2
0 1 3
0 2 3
1 2 3
0 1 4
0 2 4
0 3 4
1 2 4
1 3 4
2 3 4
可知，t=2时，${C}_{2}^{2}$=1，t=3时，${C}_{3}^{2}$=3，t=4时，${C}_{4}^{2}$=6，t=5时，${C}_{5}^{2}$=10；
故a21=30+31+36=733；
故答案为：733．
点评 本题考查了数列思想的应用及归纳推理的应用，属于中档题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
12．函数y=$\frac{1}{2}$（ex+e-x）的导数是（ ）
| A． | $\frac{1}{2}$（e x-e -x） | B． | $\frac{1}{2}$（e x+e -x） | C． | e x-e -x | D． | e x+e -x |
11．
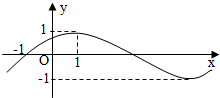已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin$\frac{π}{8}$（x+1） | B． | g（x）=sin（$\frac{π}{2}$x-$\frac{π}{4}$） | C． | g（x）=sin（$\frac{π}{8}$x+1） | D． | g（x）=sin（$\frac{π}{2}$x+$\frac{π}{4}$） |