题目内容
5.若函数f(x)=x3+ax2+1恰好有三个单调区间,则实数a的取值范围为a≠0.分析 求f(x)的导数f′(x),令f′(x)=0有两个不相等的实数根,解得a的取值范围.
解答 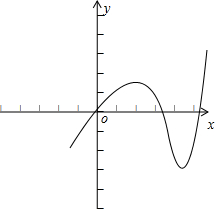 解:∵f(x)=x3+ax2+1,∴f′(x)=3x2+2ax;
解:∵f(x)=x3+ax2+1,∴f′(x)=3x2+2ax;
又f(x)有三个单调区间,如图:
∴f′(x)=0有两个不相等的实数根;
其中一个根为0,则另一个根不为0即可.所以$-\frac{3}{2a}≠0$
∴a的取值范围是:{a|a≠0}.
故答案为:a≠0.
点评 本题考查了利用函数的导数来判定函数的单调性问题,是中档题.

练习册系列答案
相关题目
16. 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )| A. | 100$\sqrt{3}$ m | B. | 100$\sqrt{2}$ m | C. | 50$\sqrt{2}$ m | D. | 25$\sqrt{2}$ m |
20.某几何体的三视图所示,且该几何体的体积是4,则正视图中的x的值是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |