��Ŀ����
15���躯��f��x��=ex-ax������e����Ȼ�����ĵ�����a��R����1��������y=f��x����ͼ����x=ln2��������l����б��Ϊ0��������l�ķ��̣�
��2���Ǻ���y=f��x��ͼ��Ϊ����C�����A��x1��f��x1������B��x2��f��x2������x1��x2��������C�ϲ�ͬ�������㣬��MΪ�߶�AB���е㣬����M��x��Ĵ��߽�����C�ڵ�N����ֱ��AB��б��Ϊk����x1=-x2�����ʣ�����C�ڵ�N���������Ƿ�ƽ����ֱ��AB����˵�����ɣ�
���� ��1�����������ú���y=f��x����ͼ����x=ln2��������l����б��Ϊ0�����a������������l�ķ��̣�
��2������߶�AB���е�M�����꣬�õ�N�����꣬������ʽ���AB��б�ʣ����ɵ����õ�����C��N������ߵ�б�ʣ���б����ȵ�$\frac{{e}^{{x}_{2}}-{e}^{{x}_{1}}}{2{x}_{2}}$-a=1-a�����캯����ȷ�������ԣ����ɵó����ۣ�
��� �⣺f�䣨x��=ex-a��----��1�֣�
��1���ɺ���y=f��x����ͼ����x=ln2��������l����б��Ϊ0��
��f�䣨ln2��=tan0=0��
��eln2-a=0����a=2��---��3�֣�
��f��ln2��=2-2ln2��
������l�ķ���Ϊy=2-2ln2��----��5�֣�
��2��������֪x1=-x2��k=$\frac{{e}^{{x}_{2}}-{e}^{{x}_{1}}}{{x}_{2}-{x}_{1}}$-a=$\frac{{e}^{{x}_{2}}-{e}^{{x}_{1}}}{2{x}_{2}}$-a��----��8�֣�
��N�ĺ�����$\frac{{x}_{1}+{x}_{2}}{2}$=0Ϊ��
����C�ڵ�N������б��k��=f�䣨0��=1-a��----��10�֣�
��������C�ڵ�N��������ƽ����ֱ��AB��
��$\frac{{e}^{{x}_{2}}-{e}^{{x}_{1}}}{2{x}_{2}}$-a=1-a����${e}^{{x}_{2}}$-$\frac{1}{{e}^{{x}_{2}}}$-2x2=0������x2��0��----��12�֣�
��g��x��=ex-$\frac{1}{{e}^{x}}$-2x��x��0����g�䣨x��=��=ex+$\frac{1}{{e}^{x}}$-2��0��
��g��x���ڣ�0��+�ޣ��ϵ�����������g��x����g��0��=0��----��14�֣�
��${e}^{{x}_{2}}$-$\frac{1}{{e}^{{x}_{2}}}$-2x2=0��������
�������C�ڵ�N�������߲�ƽ����ֱ��AB��----��16�֣�
���� ���⿼�����õ������������߷��̣�ѵ�������ù��캯����֤�����⣬��ѹ���⣮

| A�� | -$\frac{\sqrt{5}}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{3}$ | D�� | -$\frac{2}{3}$ |
| A�� | 100�� | B�� | 110�� | C�� | 120�� | D�� | 180�� |
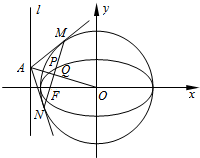 ��ƽ��ֱ������ϵxoy�У�����ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0������ΪF������Ϊl��PΪ��ԲC������һ�㣬ֱ��OQ��FP������ΪQ��ֱ��OQ��l���ڵ�A��
��ƽ��ֱ������ϵxoy�У�����ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0������ΪF������Ϊl��PΪ��ԲC������һ�㣬ֱ��OQ��FP������ΪQ��ֱ��OQ��l���ڵ�A��