题目内容
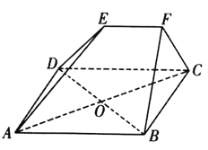
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为等边三角形,点
为等边三角形,点![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)可证![]() ,再利用平面
,再利用平面![]() 平面
平面![]() 证得
证得![]() 平面
平面![]() ,通过证明
,通过证明![]() ,可得要求证的线面垂直.
,可得要求证的线面垂直.
(2)建立空间直角坐标系,求出平面![]() 的法向量和平面
的法向量和平面![]() 的一个法向量后可求二面角
的一个法向量后可求二面角![]() 的余弦值.
的余弦值.
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() 且
且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因为菱形![]() ,所以
,所以![]() .
.
所以![]() ,
,![]() ,
,![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() ,如图所示,
,如图所示,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由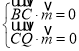 得
得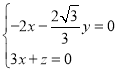 ,
,
取![]() ,可得
,可得![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则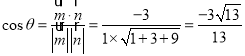 ,
,
因为二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】从2016年到2019年的某城市方便面销量情况如图所示:
年份 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 1 | 2 | 3 | 4 |
年销量 | 462 | 444 | 404 | 385 |
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2020年(
.用所求回归方程预测2020年(![]() )方便面在该城市的年销量;
)方便面在该城市的年销量;
(2)某媒体记者随机对身边的10位朋友做了一次调查,其中3位受访者认为方便面是健康食品.现从这10人中抽取3人进行深度访谈,记![]() 表示随机抽取的3人认为方便面是健康食品的人数,求随机变量
表示随机抽取的3人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中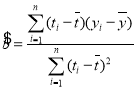 ,
,![]() .
.
参考数据:![]() .
.