题目内容
3.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,P是椭圆上一点,且△PF1F2面积的最大值等于$\sqrt{3}$.(Ⅰ)求椭圆E的方程;
(Ⅱ)直线l:y=kx+m与以线段F1F2为直径的圆O相切,并与椭圆E相交于不同的两点A、B,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{3}{2}$.求k的值.
分析 (I)由△PF1F2面积的最大值等于$\sqrt{3}$,可得bc=$\sqrt{3}$,利用离心率为$\frac{1}{2}$,可得$\frac{c}{a}$=$\frac{1}{2}$,即可求椭圆E的方程;
(II)由于圆O是以F1,F2为直径的圆,直线l:y=kx+m与⊙O相切,利用直线与圆相切的从要条件得到一个等式,把直线方程与椭圆方程联立利用整体代换的思想,根据$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{3}{2}$建立k的方程求k.
解答 解:(1)由△PF1F2面积的最大值等于$\sqrt{3}$,可得bc=$\sqrt{3}$,
∵离心率为$\frac{1}{2}$,∴$\frac{c}{a}$=$\frac{1}{2}$,解得:a=2,b=$\sqrt{3}$,
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(II)由直线l与圆O相切,得:$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,∴m2=1+k2,
设A(x1,y1)B(x2,y2),
由直线代入椭圆方程,整理得:(3+4k2)x2+8kmx+4m2-12=0,
∴x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
=k2×$\frac{4{m}^{2}-12}{3+4{k}^{2}}$+km(-$\frac{8km}{3+4{k}^{2}}$)+m2
=$\frac{3{m}^{2}-12{k}^{2}}{3+4{k}^{2}}$,
∴x1x2+y1y2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$+$\frac{3{m}^{2}-12{k}^{2}}{3+4{k}^{2}}$=$\frac{-5-5{k}^{2}}{3+4{k}^{2}}$=-$\frac{3}{2}$,
解得:k=±$\frac{\sqrt{2}}{2}$.
点评 此题考查了椭圆的基本性质及椭圆的标准方程,还考查了直线方程与椭圆方程联立之后的整体代换设而不求,还有求解问题时方程的思想.

| A. | $\frac{7}{4}$ | B. | $\frac{127}{64}$ | C. | $\frac{9}{4}$ | D. | $\frac{129}{64}$ |
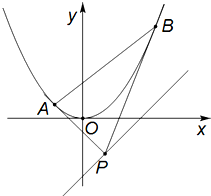 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,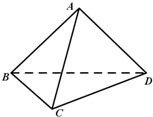 如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.
如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.