题目内容
8.过椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的右焦点F2作直线l交椭圆于A、B两点,F1是椭圆的左焦点,则△AF1B 的周长为( )| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
分析 求得椭圆的a=4,再由椭圆的定义可得△AF1B的周长为c=4a=16.
解答 解:椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的a=4,
由椭圆的定义可得,
△AF1B的周长为c=|AB|+|AF1|+|BF1|
=(|AF2|+|AF1|)+(|BF1|+|BF2|)
=2a+2a=4a=16.
故选:B.
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆的定义的运用,考查运算能力,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
16.四面体ABCD的外接球为O,AD⊥平面ABC,AD=2,△ABC为边长为3的正三角形,则球O的表面积为( )
| A. | 32π | B. | 16π | C. | 12π | D. | $\frac{32}{3}$π |
3.下列函数中既是奇函数又是增函数的是( )
| A. | y=3x+1 | B. | y=2-x-2x | C. | y=x2+1 | D. | y=x|x| |
20.在△ABC中,a,b,c分别为角A,B,C所对的边,且ccosA=b,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
17.过点P(2,3),并且在两坐标轴上的截距相等的直线方程是( )
| A. | x-y+1=0 | B. | x-y+1=0或3x-2y=0 | ||
| C. | x+y-5=0 | D. | x+y-5=0或3x-2y=0 |
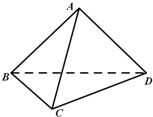 如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.
如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.