题目内容
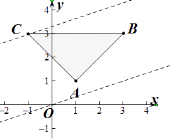
【题目】在直角坐标系xOy中,已知点A(1,1),B(3,3),点C在第二象限,且△ABC是以∠BAC为直角的等腰直角三角形.点P(x,y)在△ABC三边围城的区域内(含边界).
(1)若 ![]() +
+ ![]() +
+ ![]() =
= ![]() 求|
求| ![]() |;
|;
(2)设 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求m+2n的最大值.
(m,n∈R),求m+2n的最大值.
【答案】
(1)解:设C(a,b),a<0,b>0,
∵A(1,1),B(3,3),
∴ ![]() =(2,2),
=(2,2), ![]() =(a﹣1,b﹣1),
=(a﹣1,b﹣1),
∵△ABC是以∠BAC为直角的等腰直角三角形,
∴| ![]() |=|
|=| ![]() |,
|, ![]()
![]() =0,
=0,
∴ ![]() ,
,
解得a=﹣1,b=3
∴C(﹣1,3),
设P(x,y),
∵ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
∴(1﹣x,1﹣y)+(3﹣x,3﹣y)+(﹣1﹣x,3﹣y)=(0,0),
∴3﹣3x=0,7﹣3y=0
∴x=1,y= ![]() ,
,
∴P(1, ![]() ),
),
∴| ![]() |=
|= ![]() =
= ![]()
(2)解:∵ ![]() =(﹣2,2),
=(﹣2,2), ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),
(m,n∈R),
∴(x,y)=m(2,2)+n(﹣2,2)=(2m﹣2n,2m+2n),
∴x=2m﹣2n,y=2m+2n,
∴m= ![]() (x+y),2n=
(x+y),2n= ![]() (y﹣x),
(y﹣x),
∴m+2n=﹣ ![]() x+
x+ ![]() y,
y,
设z=3y﹣x,直线z=3y﹣x经过点C(﹣1,3)时,z取得最大值,
即m+2n= ![]() +
+ ![]() ×3=
×3= ![]()
【解析】(1)设C(a,b),a<0,b>0,根据向量的坐标运算和向量的模,以及向量的垂直的条件求出点C的坐标,再根据向量的加减运算求出P的坐标,问题得以解决,(2)根据向量的坐标运算,以及线性规划,即可求出答案.
【考点精析】通过灵活运用平面向量的基本定理及其意义,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
相关题目
