题目内容
【题目】已知函数f(x)=ex﹣ax﹣1,g(x)=lnx﹣ax+a,若存在x0∈(1,2),使得f(x0)g(x0)<0,则实数a的取值范围是( )
A.![]()
B.(ln2,e﹣1)
C.[1,e﹣1)
D.![]()
【答案】A
【解析】解:由 ![]()
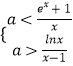
![]() <a<
<a< ![]() ,
,
令F(x)= ![]() ,则F′(x)=
,则F′(x)= ![]() <0对x∈(1,2)成立,
<0对x∈(1,2)成立,
∴F(x)在(1,2)递减,
∴F(x)min=F(2)=ln2,
令G(x)= ![]() ,则G′(x)=
,则G′(x)= ![]() >0对x∈(1,2)成立,
>0对x∈(1,2)成立,
∴G(x)在(1,2)上递增,
∴G(x)max=G(2)= ![]() ,
,
若存在x0∈(1,2),使得f(x0)g(x0)<0,
则ln2<a< ![]() 时,满足题意,
时,满足题意,
故选:A.
【考点精析】认真审题,首先需要了解函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法).

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目