题目内容
【题目】如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1 , y1)到准线l的距离为d,且d=λp(λ>0). 
(1)若y1=d=1,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率为定值.
,求证:直线AB的斜率为定值.
【答案】
(1)解:由条件知,x1=1﹣ ![]() ,则A点坐标为(1﹣
,则A点坐标为(1﹣ ![]() ,1),代入抛物线方程得p=1,
,1),代入抛物线方程得p=1,
∴抛物线方程为y2=2x,
(2)证明:设B(x2,y2),直线AB的方程为y=k(x+ ![]() ),
),
将直线AB的方程代入y2=2px,消去y得: ![]() ,
,
解得:x1= 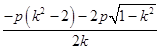 ,x2=
,x2= 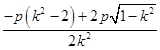 .
.
∵d=λp,
∴ ![]() ,
,
![]() +λ
+λ ![]() =
= ![]() ,
, ![]() ,
,
∴p=x2﹣x1= ![]() ,
,
∴ ![]() ,
,
∴直线AB的斜率为定值.
【解析】(1)由题意可知x1=1﹣ ![]() ,A点坐标为(1﹣
,A点坐标为(1﹣ ![]() ,1),将A点坐标代入抛物线方程求得p的值,写出抛物线的标准方程;(2)直线AB过M(﹣
,1),将A点坐标代入抛物线方程求得p的值,写出抛物线的标准方程;(2)直线AB过M(﹣ ![]() ,0),设直线AB的方程为y=k(x+
,0),设直线AB的方程为y=k(x+ ![]() ),代入抛物线方程y2=2px,消去y,整理得
),代入抛物线方程y2=2px,消去y,整理得 ![]() ,解出x1、x2,将d=x1+
,解出x1、x2,将d=x1+ ![]() ,代入d=λp,得
,代入d=λp,得 ![]() ,
, ![]() +λ
+λ ![]() =
= ![]() ,可知,
,可知, ![]() ,将x1、x2代入,即可解得
,将x1、x2代入,即可解得 ![]() ,可证直线AB的斜率为定值.
,可证直线AB的斜率为定值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




