题目内容
18.已知函数f(x)=2cosx(sinx+cosx),x∈R.(1)求函数f(x)的单调递增区间;
(2)求函数f(x)在区间$[{0,\frac{π}{2}}]$上的最大值和最小值.
分析 (1)由三角函数恒等变换的应用化简解析式可得f(x)=$\sqrt{2}sin({2x+\frac{π}{4}})+1$,由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$,解得函数单调递增区间.
(2)由$0≤x≤\frac{π}{2}$可求$0≤2x+\frac{π}{4}≤\frac{5π}{4}$,利用正弦函数的图象和性质即可得解.
解答 解:(1)f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+cos2x+1=$\sqrt{2}sin({2x+\frac{π}{4}})+1$…(4分)
由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$,解得$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}$
所以函数f(x)单调递增区间为$[{kπ-\frac{3π}{8},kπ+\frac{π}{8}}]({k∈Z})$…(7分)
(2)当$0≤x≤\frac{π}{2}$时$0≤2x+\frac{π}{4}≤\frac{5π}{4}$,
所以当$2x+\frac{π}{4}=\frac{π}{2}$即$x=\frac{π}{8}$时,函数f(x)取得最大值$\sqrt{2}+1$,
当$2x+\frac{π}{4}=\frac{5π}{4}$即$x=\frac{π}{2}$时,函数f(x)取得最小值0…(14分)
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的单调性,三角函数的最值的求法,属于基本知识的考查.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.$\frac{27π}{4}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
3.A={x||x-1|≥1,x∈R},B={x|log2x>1,x∈R},则“x∈A”是“x∈B”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分也非必要条件 |
10.已知x=lnπ,y=log${\;}_{\frac{1}{2}}$π,z=e${\;}^{-\frac{1}{2}}$,则( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
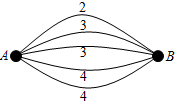 如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.
如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.