题目内容
6.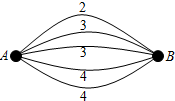 如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.
如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.(1)设选取的2条网线由A到B通过的信息总量为x,当x≥6时,则保证信息畅通.求线路信息畅通的概率;
(2)求选取的2条网线可通过信息总量的数学期望.
分析 (1)随机任取2条网线共有10种不同的情况,直接求解概率即可.
(2)求出选取的2条网线的概率,利用数学期望求解即可.
解答 (理科)解:(1)随机任取2条网线共有10种不同的情况.
∵2+4=3+3=6,
∴$P(x=6)=\frac{2+1}{10}=\frac{3}{10}$,…2'
∵3+4=7,∴$P(x=7)=\frac{4}{10}$,…4'
∵4+4=8,∴$P(x=8)=\frac{1}{10}$,…6'
∴$P(x≥6)=\frac{3}{10}+\frac{4}{10}+\frac{1}{10}=\frac{8}{10}=\frac{4}{5}$…8'
(2)∵$2+3=5,P(x=5)=\frac{2}{10}=\frac{1}{5}$,…10'
∴线路通过信息量的数学期望是$E(x)=5×\frac{1}{5}+6×\frac{3}{10}+7×\frac{4}{10}+8×\frac{1}{10}=6.4$…13'
答:(1)线路信息畅通的概率是$\frac{4}{5}$; (2)线路通过信息量的数学期望是6.4…14'
点评 本题考查离散型随机变量的期望的求法,考查计算能力.

练习册系列答案
相关题目
17.已知f(x)=ex+sinx,则f′(x)=( )
| A. | lnx+cosx | B. | lnx-cosx | C. | ex+cosx | D. | ex-cosx |
14.已知等差数列{an}中,a1+a5=6,则a1+a2+a3+a4+a5=( )
| A. | 10$\sqrt{6}$ | B. | 5$\sqrt{6}$ | C. | 30 | D. | 15 |
15.设z1=-3+4i,z2=2-3i,则z1+z2在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
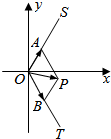 如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.
如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.