题目内容
【题目】设定义域为R的函数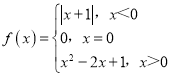 .
.
(1)在平面直角坐标系中作出函数f(x)的图象,并指出f(x)的单调区间(不需证明);
(2)若方程f(x)+5a=0有两个解,求出a的取值范围(不需严格证明,简单说明即可);
(3)设定义域为R的函数g(x)为偶函数,且当x≥0时,g(x)=f(x),求g(x)的解析式.
【答案】(1)函数f(x)的增区间为(﹣1,0),(1,+∞);减区间为(﹣∞,﹣1),(0,1),图象见解析
(2)![]()
(3)
【解析】
(1)作出函数f(x)的图象,由图象即可观察得出;
(2)方程f(x)+5a=0有两个解,等价于函数f(x)的图象与直线![]() 有两个交点,由图即可求出;
有两个交点,由图即可求出;
(3)先求出x≥0时,g(x)的解析式,再根据偶函数的性质,求出x<0时,g(x)
的解析式,即可求出定义在![]() 上的g(x)的解析式.
上的g(x)的解析式.
(1)作出函数f(x)的图象,如图所示:
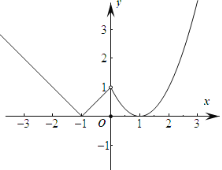
函数f(x)的增区间为(﹣1,0),(1,+∞),减区间为(﹣∞,﹣1),(0,1).
(2)要使方程f(x)+5a=0有两个解,等价于函数f(x)的图象与直线![]() 有两个交点,由图可知,﹣5a≥1,解得
有两个交点,由图可知,﹣5a≥1,解得![]() .故实数a的取值范围为
.故实数a的取值范围为![]() ;
;
(3)由题意,当x=0时,g(x)=0,当x>0时,g(x)=x2﹣2x+1,
设x<0,则﹣x>0,故g(﹣x)=(﹣x)2﹣2(﹣x)+1=x2+2x+1,
又函数g(x)为偶函数,故g(x)=g(﹣x)=x2+2x+1(x<0),
综上,函数g(x)的解析式为 .
.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(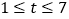 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: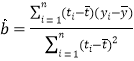 ,
,![]() .
.



