题目内容
7．命题p：若sinx＞siny，则x＞y；命题q：x2+y2≥2xy，下列命题为假命题的是（ ）| A． | p或q | B． | p且q | C． | q | D． | ￢p |
分析 根据正弦函数的图象即可判断出sinx＞siny时，不一定得到x＞y，所以说命题p是假命题，而根据基本不等式即可判断出命题q为真命题，然后根据￢p，p或q，p且q的真假和p，q真假的关系即可找出正确选项．
解答 解：x=$\frac{π}{2}$，y=π，满足sinx＞siny，但x＜y；
∴命题p是假命题；
x2+y2≥2xy，这是基本不等式；
∴命题q是真命题；
∴p或q为真命题，p且q为假命题，q是真命题，￢p是真命题；
∴是假命题的是B．
故选B．
点评 考查正弦函数的图象，能够取特殊角以说明命题p是假命题，熟悉基本不等式：a2+b2≥2ab，a=b时取“=”，以及￢p，p或q，p且q的真假和p，q真假的关系．
练习册系列答案
相关题目
18．
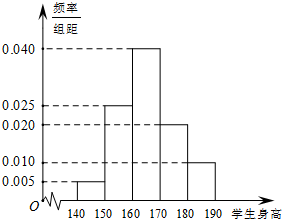为调查学生身高的情况，随机抽测了高三两个班120名学生的身高（单位：cm），所得数据均在区间[140，190]上，其频率分布直方图如图所示（左下），则在抽测的120名学生中，身高位于区间[160，180）上的人数为（ ）
为调查学生身高的情况，随机抽测了高三两个班120名学生的身高（单位：cm），所得数据均在区间[140，190]上，其频率分布直方图如图所示（左下），则在抽测的120名学生中，身高位于区间[160，180）上的人数为（ ）| A． | 70 | B． | 71 | C． | 72 | D． | 73 |
为了解一种植物的生长情况，抽取一批该植物样本测量高度（单位：cm），其频率分布直方图如图所示
19．在△ABC中，角A，B，C所对的边长为a，b，c，若a=$\sqrt{2}$，b=2，sinB+cosB=$\sqrt{2}$，则A=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{2π}{3}$ |
17．已知集合M={x|$\frac{1+x}{1-x}$＞0}，则∁RM=（ ）
| A． | {x|-1≤x＜1} | B． | {x|-1≤x≤1} | C． | {x|x≤-1或x＞1} | D． | {x|x≤-1或x≥1} |