题目内容
19.在△ABC中,角A,B,C所对的边长为a,b,c,若a=$\sqrt{2}$,b=2,sinB+cosB=$\sqrt{2}$,则A=( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
分析 先利用辅助角公式求出角B,然后利用正弦定理求出角A即可,注意三角形的内角和为180°.
解答 解:∵sinB+cosB=$\sqrt{2}$,即$\sqrt{2}$($\frac{\sqrt{2}}{2}$sinB+$\frac{\sqrt{2}}{2}$cosB)=$\sqrt{2}$,
∴$\sqrt{2}$sin(B+$\frac{π}{4}$)=$\sqrt{2}$,解得sin(B+$\frac{π}{4}$)=1,
∴结合B的范围可得:B=$\frac{π}{4}$,则sinB=$\frac{\sqrt{2}}{2}$,
根据正弦定理$\frac{\sqrt{2}}{sinA}$=$\frac{2}{\frac{\sqrt{2}}{2}}$,
解得sinA=$\frac{1}{2}$,解得A=$\frac{π}{6}$或$\frac{5π}{6}$(舍去),
故选:B.
点评 本题主要考查了辅助角公式,以及正弦定理的应用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.设复数z≠-1,则“|z|=1”是“$\frac{z-1}{z+1}$是纯虚数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.命题p:若sinx>siny,则x>y;命题q:x2+y2≥2xy,下列命题为假命题的是( )
| A. | p或q | B. | p且q | C. | q | D. | ¬p |
4.执行如图所示的程序框图,若输出s的值为70,则判断框内可填入的条件是( )
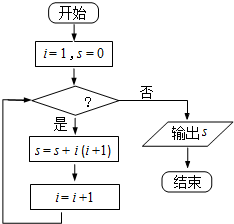

| A. | i≤5 | B. | i<5 | C. | i>5 | D. | i≥5 |
8. 如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )
如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )
 如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )
如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )| A. | O是△AEF的垂心 | B. | O是△AEF的内心 | C. | O是△AEF的外心 | D. | O是△AEF的重心 |