题目内容
等差数列中a2与a6的等差中项为5,a3与a7的等差中项为7,则an=______.
由题意可得:a2+a6=2×5,a3+a7=2×7,
由等差数列的性质可得2a4=a2+a6=10,2a5=a3+a7=14
解之可得a4=5,a5=7,故公差d=a5-a4=2
故a1=a4-3d=5-6=-1,
故an=-1+2(n-1)=2n-3
故答案为:2n-3
由等差数列的性质可得2a4=a2+a6=10,2a5=a3+a7=14
解之可得a4=5,a5=7,故公差d=a5-a4=2
故a1=a4-3d=5-6=-1,
故an=-1+2(n-1)=2n-3
故答案为:2n-3

练习册系列答案
相关题目
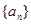 中,
中,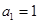 ,
,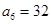 ,
, 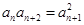 (
(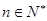 ),把数列的各项按如下方法进行分组:(
),把数列的各项按如下方法进行分组:(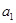 )、(
)、(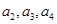 )、(
)、(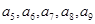 )、 ,记
)、 ,记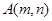 为第
为第 组的第
组的第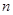 个数(从前到后),若
个数(从前到后),若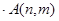 =
=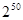 ,则
,则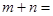 _________.
_________.