题目内容
4.如图,在四边形ABCD中,∠B=∠C=60°,BC=1,以CD为直径作圆与AB相切于点M,且交BC边于E点,求BE的长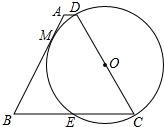
分析 连接OE,OM,延长CD,BA交于点G,由∠B=∠C=60°,易得∠G=60°,△CEO为等边三角形,由同位角相等易得OE∥BG,利用平行线分线段成比例定理可得$\frac{CE}{BE}=\frac{OC}{OG}$,在Rt△OMG中,利用锐角三角函数可得OG,从而得到$\frac{CE}{BE}$,由CE+BE=BC=1,解得BE.
解答  解:设⊙O的半径为r,
解:设⊙O的半径为r,
连接OE,OM,延长CD,BA交于点G,
∵∠B=∠C=60°,
∴∠G=60°,
∵OC=OE=r,
∴∠CEO=60°,
∴△CEO为等边三角形,
∴CE=OC=r,
∵∠OEC=∠B=60°,
∴OE∥BG,
∴$\frac{CE}{BE}=\frac{OC}{OG}$,
在Rt△OMG中,OG=$\frac{OM}{sin60°}$=$\frac{2\sqrt{3}}{3}$r,
则$\frac{CE}{BE}$=$\frac{r}{\frac{2\sqrt{3}}{3}r}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{3}}{2}$BE+BE=1,
∴BE=4-2$\sqrt{3}$.
点评 本题主要考查了等边三角形的判定及性质,平行线分线段成比例定理等,作出适当的辅助线,构建直角三角形是解答此题的关键.

练习册系列答案
相关题目
14.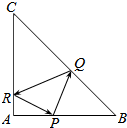 在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
 在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )| A. | $\frac{4}{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |