题目内容
14.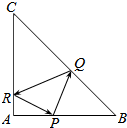 在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )
在直角三角形△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的内心,则AP等于( )| A. | $\frac{4}{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |
分析 建立坐标系,设点P的坐标,可得P关于直线BC的对称点P1的坐标,和P关于y轴的对称点P2的坐标,由P1,Q,R,P2四点共线可得直线的方程,由于过△ABC的内心,代入可得关于a的方程,解之可得P的坐标,进而可得AP的值.
解答  解:建立如图所示的坐标系:
解:建立如图所示的坐标系:
可得B(4,0),C(0,4),故直线BC的方程为x+y=4,
设△ABC的内切圆的半径为r,则$\frac{1}{2}×4×4=\frac{1}{2}×(4+4+4\sqrt{2})r$,
∴r=4-2$\sqrt{2}$,
∴△ABC的内心坐标为(4-2$\sqrt{2}$,4-2$\sqrt{2}$).
设P(a,0),其中0<a<4,
则点P关于直线BC的对称点P1(x,y),满足$\left\{\begin{array}{l}{\frac{a+x}{2}+\frac{y+0}{2}=4}\\{\frac{y-0}{x-a}•(-1)=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=4-a}\end{array}\right.$,即P1(4,4-a),
易得P关于y轴的对称点P2(-a,0),
由光的反射原理可知P1,Q,R,P2四点共线,
直线QR的斜率为k=$\frac{4-a}{4+a}$,故直线QR的方程为y=$\frac{4-a}{4+a}$(x+a),
由于直线QR过△ABC的内心,代入化简可得a=4$\sqrt{2}$-4,
故AP=4$\sqrt{2}$-4.
故选:D.
点评 本题考查直线与点的对称问题,涉及直线方程的求解以及光的反射原理的应用,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
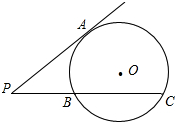 如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
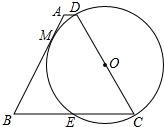
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值. 如图,AC为⊙O的直径,弦BD⊥AC交与点P,PC=1,PA=4,则sin∠ABD的值为$\frac{2\sqrt{5}}{5}$.
如图,AC为⊙O的直径,弦BD⊥AC交与点P,PC=1,PA=4,则sin∠ABD的值为$\frac{2\sqrt{5}}{5}$.