题目内容
14.作出下列函数的图象(1)y=$\frac{2-x}{x+1}$
(2)y=($\frac{1}{2}$)|x+1|
(3)y=|log2x-1|.
分析 利用基本函数的图象,结合图象变换,即可得出结论.
解答 解:(1)y=$\frac{2-x}{x+1}$=-1+$\frac{3}{x+1}$,由y=$\frac{3}{x}$的图象向左平移1个单位,再向下平移1个单位得到,如图所示.
(2)先作出y=($\frac{1}{2}$)|x|的图象,再向左平移1个单位得到,如图所示.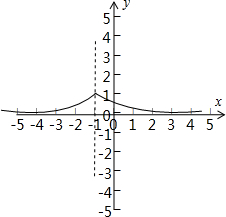
(3)先作出y=log2x的图象,再将其图象向下平移1个单位长度,保留x轴上方的部分,将x轴下方的图象翻折到x轴上方,即得y=|log2x-1|的图象,如图所示.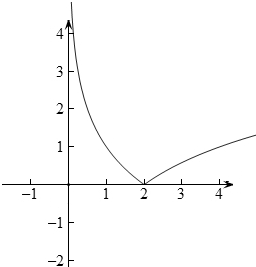
点评 本题主要考查了的图象的画法,考查图象变换,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知函数f(x)=log2(ax2+ax+1)的值域为R,则实数a的取值范围是( )
| A. | (4,+∞) | B. | (-∞,4) | C. | [4,+∞) | D. | (-∞,4] |
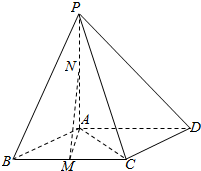 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD点M,N分别是BC,PA的中点,且PA=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD点M,N分别是BC,PA的中点,且PA=PB=2.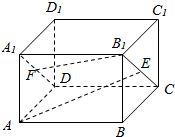 如图,在长方体ABCD-A1B1C1D1中,E是矩形BCC1B1的中点,F是矩形ADD1A1的中心,连接AE,B1F,判断AE与B1F是否为异面直线.
如图,在长方体ABCD-A1B1C1D1中,E是矩形BCC1B1的中点,F是矩形ADD1A1的中心,连接AE,B1F,判断AE与B1F是否为异面直线.