题目内容
若函数f(x)=
sin2x+sinx,则f′(x)是( )
| 1 |
| 2 |
| A.仅有最小值的奇函数 |
| B.仅有最大值的偶函数 |
| C.既有最大值又有最小值的偶函数 |
| D.非奇非偶函数 |
∵函数f(x)=
sin2x+sinx,
∴f′(x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+
)2-
,当cosx=-
时,f′(x)取得最小值-
;当cosx=1时,f′(x)取得最大值2.
且f′(-x)=f′(x).即f′(x)是既有最大值,又有最小值的偶函数.
故选C.
| 1 |
| 2 |
∴f′(x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+
| 1 |
| 4 |
| 9 |
| 8 |
| 1 |
| 4 |
| 9 |
| 8 |
且f′(-x)=f′(x).即f′(x)是既有最大值,又有最小值的偶函数.
故选C.

练习册系列答案
相关题目
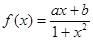 是定义在
是定义在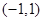 上的奇函数,且
上的奇函数,且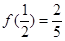 .
.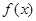 的解析式;
的解析式;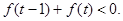 .
.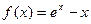 (
(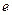 为自然对数的底数)
为自然对数的底数)
 (Ⅰ)求
(Ⅰ)求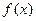 的最小值
的最小值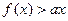 的解集为P,且
的解集为P,且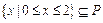 ,求实数a的取值范围
,求实数a的取值范围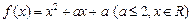 ,
,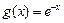 ,
,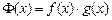 .
.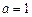 时,求
时,求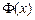 的单调区间;
的单调区间;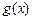 在点
在点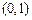 处的切线与直线
处的切线与直线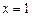 及曲线
及曲线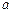 ,使
,使