题目内容
数列{an}是公差为d的等差数列，函数f（x）=（x-a1）（x-a2）（x-a3）（x-a4），则f′（a1）+f′（a2）+f′（a3）+f′（a4）=______．
因为f（x）=（x-a1）（x-a2）（x-a3）（x-a4），
所以f'（x）=[（x-a2）（x-a3）（x-a4）]+（x-a1）+[（x-a2）（x-a3）（x-a4）]'，
所以f′（a1）=（a1-a2）（a1-a3）（a1-a4）．
因为数列{an}是公差为d的等差数列，所以f′（a1）=（a1-a2）（a1-a3）（a1-a4）=（-d）（-2d）（-3d）=-6d3．
同理f′（a2）=（a2-a1）（a2-a3）（a2-a4）=2d3．
f′（a3）=（a3-a2）（a3-a1）（a3-a4）=-2d3．
f′（a4）=（a4-a2）（a4-a3）（a4-a1）=6d3．
所以f′（a1）+f′（a2）+f′（a3）+f′（a4）=-6d3+2d3-2d3+6d3=0．
故答案为：0
所以f'（x）=[（x-a2）（x-a3）（x-a4）]+（x-a1）+[（x-a2）（x-a3）（x-a4）]'，
所以f′（a1）=（a1-a2）（a1-a3）（a1-a4）．
因为数列{an}是公差为d的等差数列，所以f′（a1）=（a1-a2）（a1-a3）（a1-a4）=（-d）（-2d）（-3d）=-6d3．
同理f′（a2）=（a2-a1）（a2-a3）（a2-a4）=2d3．
f′（a3）=（a3-a2）（a3-a1）（a3-a4）=-2d3．
f′（a4）=（a4-a2）（a4-a3）（a4-a1）=6d3．
所以f′（a1）+f′（a2）+f′（a3）+f′（a4）=-6d3+2d3-2d3+6d3=0．
故答案为：0
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
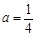时，求函数y=f(x)的极值；
．
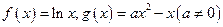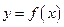与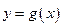
的图象在公共点P处有相同的切线，求实数
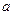的值并求点P的坐标；（2）若函数
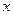轴的垂线分别与
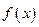的图像和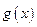
的图像交S、T点，以S为切点作
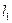，以T为切点作
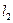．是否存在实数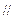
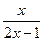在点（1，1）处的切线方程为( )