题目内容
若f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2009′(x)=______.
由题意f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=-sinx,f3(x)=f2′(x)=-cosx,f4(x)=f3′(x)=sinx,由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,
∵2009=4×502+1,f2009(x)是一周中的第一个函数,故f2009(x)=cosx
故答案为cosx
∵2009=4×502+1,f2009(x)是一周中的第一个函数,故f2009(x)=cosx
故答案为cosx

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
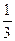 时, 函数取得极大值, 则m的值为 ( )
时, 函数取得极大值, 则m的值为 ( )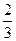
 是偶函数,
是偶函数, 是它的导函数,当
是它的导函数,当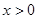 时,
时,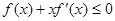 恒成立,且
恒成立,且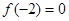 ,则不等式
,则不等式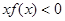 的解集为 。
的解集为 。