题目内容
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若函数![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,对于
,对于![]() ,
,![]() 的值域为
的值域为![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .有
.有![]()
![]() 求得函数
求得函数![]() .然后将函数
.然后将函数![]() 存在单调递减区间,转化为
存在单调递减区间,转化为![]() 存在取值区间求解;(2)根据
存在取值区间求解;(2)根据![]() ,求导
,求导![]() ,根据
,根据![]() ,分①当
,分①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,三种情况讨论值域,然后再分别研究
时,三种情况讨论值域,然后再分别研究![]() 成立,确定实数t范围.
成立,确定实数t范围.
因为![]() ,所以
,所以![]() ,
,
又![]() ,故
,故![]() .
.
(1)由题意得![]() ,
,
若函数![]() 存在单调减区间,
存在单调减区间,
则![]()
即![]() 存在取值区间,
存在取值区间,
即![]() 存在取值区间,
存在取值区间,
所以![]() .
.
当![]() 时,
时,![]()
当![]() ,则
,则![]() ,无解.
,无解.
当![]() ,则
,则![]() ,
,![]() .
.
当![]() ,则
,则![]() ,
,![]() 且
且![]()
所以![]() 时,函数不存在单调减区间.
时,函数不存在单调减区间.
故![]()
(2)因为![]() ,所以
,所以![]()
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,由
上单调递减,由![]() ,
,
所以![]() ,即
,即![]() ,得
,得![]() ;
;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,得
,得![]() ,
,
③当![]() 时,在
时,在![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
在![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
令![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,而
,而![]() ,所以不等式(
,所以不等式(![]() )无解,
)无解,
综上所述,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某公司组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
(1)从甲、乙两个部门所有员工中随机抽取1人,求该员工学习活跃的概率;
(2)根据表中数据判断能否有![]() 的把握认为员工学习是否活跃与部门有关;
的把握认为员工学习是否活跃与部门有关;
(3)活动第二周,公司为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?
参考公式: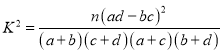 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.