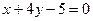题目内容
(12分)设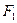 、
、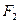 分别是椭圆
分别是椭圆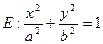 ,
,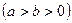
 的左、右焦点,
的左、右焦点,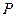 是该椭圆上一个动点,且
是该椭圆上一个动点,且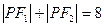 ,
,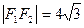 。
。
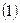 、求椭圆
、求椭圆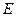 的方程;
的方程;
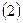 、求出以点
、求出以点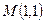 为中点的弦所在的直线方程。
为中点的弦所在的直线方程。
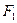 、
、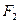 分别是椭圆
分别是椭圆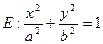 ,
,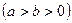
 的左、右焦点,
的左、右焦点,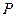 是该椭圆上一个动点,且
是该椭圆上一个动点,且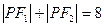 ,
,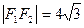 。
。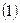 、求椭圆
、求椭圆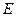 的方程;
的方程;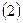 、求出以点
、求出以点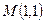 为中点的弦所在的直线方程。
为中点的弦所在的直线方程。(1)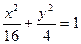 (2)
(2)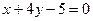
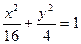 (2)
(2)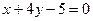
略

练习册系列答案
相关题目
题目内容
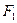 、
、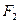 分别是椭圆
分别是椭圆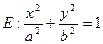 ,
,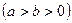
 的左、右焦点,
的左、右焦点,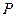 是该椭圆上一个动点,且
是该椭圆上一个动点,且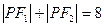 ,
,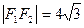 。
。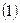 、求椭圆
、求椭圆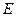 的方程;
的方程; 、求出以点
、求出以点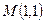 为中点的弦所在的直线方程。
为中点的弦所在的直线方程。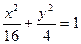 (2)
(2)