题目内容
(本小题满分13分)已知椭圆C的中心在圆点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。(I)由题意知: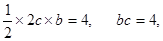
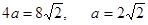 ,解得
,解得
∴椭圆的方程为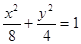 ………………………… 5分
………………………… 5分
(II)假设存在椭圆上的一点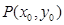 ,使得直线
,使得直线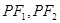 与以
与以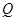 为圆心的圆相切,则
为圆心的圆相切,则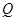 到直线
到直线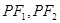 的距离相等,
的距离相等,
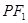 :
:  ,
, :
: 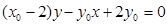
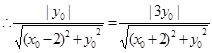 化简整理得:
化简整理得: … 9分
… 9分
∵点在椭圆上,∴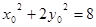 解得:
解得: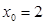 或
或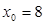 (舍)…… 11分
(舍)…… 11分
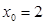 时,
时,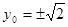 ,
,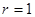 ,∴椭圆上存在点
,∴椭圆上存在点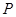 ,其坐标为
,其坐标为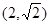 或
或 ,使得直线
,使得直线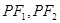 与以
与以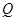 为圆心的圆
为圆心的圆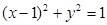 相切 ……………… 13分
相切 ……………… 13分
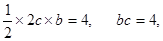
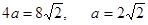 ,解得
,解得
∴椭圆的方程为
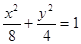 ………………………… 5分
………………………… 5分(II)假设存在椭圆上的一点
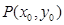 ,使得直线
,使得直线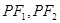 与以
与以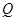 为圆心的圆相切,则
为圆心的圆相切,则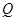 到直线
到直线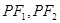 的距离相等,
的距离相等,
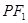 :
:  ,
, :
: 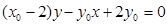
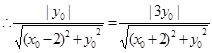 化简整理得:
化简整理得: … 9分
… 9分∵点在椭圆上,∴
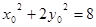 解得:
解得: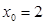 或
或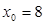 (舍)…… 11分
(舍)…… 11分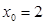 时,
时,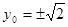 ,
,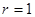 ,∴椭圆上存在点
,∴椭圆上存在点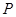 ,其坐标为
,其坐标为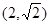 或
或 ,使得直线
,使得直线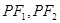 与以
与以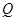 为圆心的圆
为圆心的圆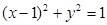 相切 ……………… 13分
相切 ……………… 13分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
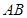 为过椭圆
为过椭圆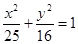 的中心的弦,
的中心的弦,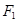 为椭圆的左焦点,则?
为椭圆的左焦点,则?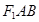 面积的最大值( )
面积的最大值( )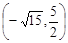 且与椭圆
且与椭圆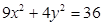 有相同焦点的椭圆方程。
有相同焦点的椭圆方程。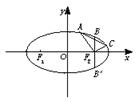
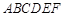 的两个顶点
的两个顶点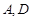 为椭圆的两个焦点,其余四个顶点在
为椭圆的两个焦点,其余四个顶点在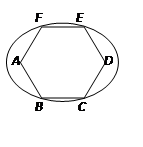





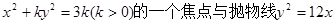 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )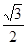

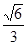
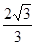
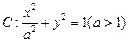 的上顶点为
的上顶点为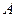 ,右焦点为
,右焦点为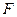 ,直线
,直线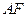 与圆
与圆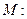
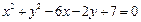 相切.
相切.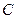 的方程;
的方程;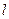 与椭圆
与椭圆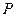 、
、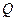 两点,且
两点,且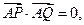 求证:直线
求证:直线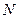 的坐标.
的坐标.
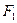 、
、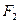 分别是椭圆
分别是椭圆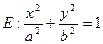 ,
,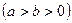
 的左、右焦点,
的左、右焦点,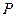 是该椭圆上一个动点,且
是该椭圆上一个动点,且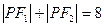 ,
,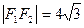 。
。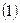 、求椭圆
、求椭圆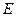 的方程;
的方程;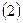 、求出以点
、求出以点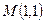 为中点的弦所在的直线方程。
为中点的弦所在的直线方程。