题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c且满足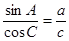 .
.
(Ⅰ)求角C的大小;
(Ⅱ)求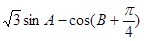 的最大值,并求取得最大值时角A的大小.
的最大值,并求取得最大值时角A的大小.
(Ⅰ) 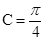 . (Ⅱ)
. (Ⅱ)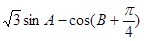 的最大值为2,此时A=
的最大值为2,此时A=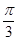 .
.
解析试题分析:(Ⅰ)由正弦定理得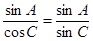 .
.
因为0<A<π,0<C<π.
所以sinA>0. 从而sinC="cosC."
又cosC≠0,所以tanC=1,则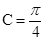 . 5分
. 5分
(Ⅱ)由(Ⅰ)知B=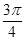 -A. 于是
-A. 于是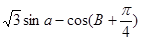
=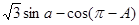
=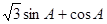
=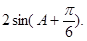
因为0<A<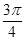 ,所以
,所以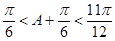 ,
,
所以当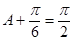 ,即A=
,即A=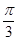 时,
时,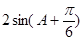 取最大值2.
取最大值2.
综上所述,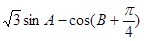 的最大值为2,此时A=
的最大值为2,此时A=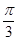 . 9分
. 9分
考点:正弦定理的应用,和差倍半的三角函数,三角函数的图象和性质。
点评:中档题,三角形中的问题,往往利用两角和与差的三角函数公式进行化简,利用正弦定理、余弦定理建立边角关系。本题综合性较强,综合考查两角和与差的三角函数,正弦定理的应用,三角函数的图象和性质。涉及角的较小范围,易于出错。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,
, ,求a,c,的值.
,求a,c,的值. 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知
 ;
; ,求
,求 的最大值.
的最大值. 的圆面,图中圆内接四边形
的圆面,图中圆内接四边形 为拟定拆迁的棚户区,测得
为拟定拆迁的棚户区,测得 百米,
百米, 百米,
百米, 百米.
百米.
 ,
, 不能变更,而边界
不能变更,而边界 ,
, 可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧 上求出一点
上求出一点 ,使得棚户区改造的新建筑用地
,使得棚户区改造的新建筑用地 的面积最大,并求最大值.
的面积最大,并求最大值. 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
. 边的长及角
边的长及角 的大小;
的大小; ,若点
,若点 ,试判断
,试判断

 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .已知
.已知 .
. ,求
,求 的最大值.
的最大值. 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
. 求
求 的长.
的长. ,
, ,
, 分别为
分别为 、
、 、
、 的对边,且
的对边,且
 ,且
,且 的面积为
的面积为 ,求
,求 的值。
的值。