题目内容
怀化市某棚户区改造工程规划用地近似为图中半径为 的圆面,图中圆内接四边形
的圆面,图中圆内接四边形 为拟定拆迁的棚户区,测得
为拟定拆迁的棚户区,测得 百米,
百米, 百米,
百米, 百米.
百米.
(Ⅰ)请计算原棚户区 的面积及圆面的半径
的面积及圆面的半径 ;
;
(Ⅱ)因地理条件的限制,边界 ,
, 不能变更,而边界
不能变更,而边界 ,
, 可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧 上求出一点
上求出一点 ,使得棚户区改造的新建筑用地
,使得棚户区改造的新建筑用地 的面积最大,并求最大值.
的面积最大,并求最大值.
(Ⅰ)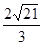 ;(Ⅱ)
;(Ⅱ)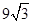 .
.
解析试题分析:(Ⅰ)可将四边形面积转化为三角形面积来求,利用余弦定理解角;(Ⅱ)将四边形面积转化为三角形面积来求,利用基本不等式求最值.
试题解析:(Ⅰ)因为四边形ABCD内接于圆,所以∠ABC+∠ADC=1800 ,连接AC,由余弦定理得: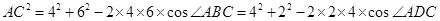
∴ ,∵
,∵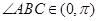 故
故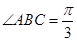
∴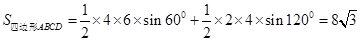 (万平方米)
(万平方米)
在△ABC中,有余弦定理求得 ,由正弦定理得:
,由正弦定理得: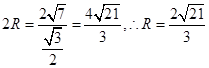 6分
6分
(Ⅱ) 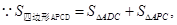 又
又
设AP=x,CP=y,则 ,由余弦定理得:
,由余弦定理得: ,
,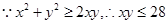 (当且仅当x=y时等号成立)
(当且仅当x=y时等号成立)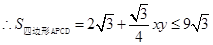
∴当P在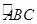 的中点时,
的中点时, 最大,最大值是
最大,最大值是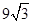 (万平方米) 13分
(万平方米) 13分
考点:解三角形,正弦定理,余弦定理,基本不等式.

练习册系列答案
相关题目
 的外接圆半径
的外接圆半径 ,角
,角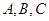 的对边分别是
的对边分别是 ,且
,且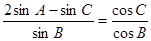
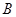 和边长
和边长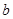 ;
;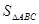 的最大值及取得最大值时的
的最大值及取得最大值时的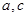 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状. 的三边为
的三边为 满足
满足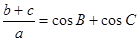 .
. 的值;
的值; 的取值范围.
的取值范围. 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
 的值;(Ⅱ)求
的值;(Ⅱ)求 边的长.
边的长. ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c. 中,
中, .
. 的大小;
的大小; ,且
,且 ,求
,求 的面积.
的面积. 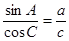 .
.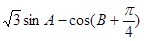 的最大值,并求取得最大值时角A的大小.
的最大值,并求取得最大值时角A的大小. 处是我舰追上敌舰的地点,且已知AB距离为12海里.
处是我舰追上敌舰的地点,且已知AB距离为12海里.
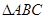 中,
中,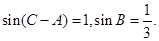
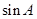 的值;
的值; ,求
,求