题目内容
某学校高一年级组建了A、B、C、D四个不同的“研究性学习”小组,要求高一年级学生必须参加,
且只能参加一个小组的活动.假定某班的甲、乙、丙三名同学对这四个小组的选择是等可能的.
(1)求甲、乙、丙三名同学选择四个小组的所有选法种数;
(2)求甲、乙、丙三名同学中至少有二人参加同一组活动的概率;
(3)设随机变量X为甲、乙、丙三名同学参加A小组活动的人数,求X的分布列与数学期望EX.
(1)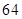 ; (2)
; (2)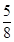 ; (3)分布列见解析,期望为
; (3)分布列见解析,期望为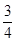 .
.
解析试题分析:(1)利用分布乘法原理三名同学先后选择共有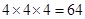 种;(2)找出三名同学中至少有二人参加同一组活动的对立面,三名同学选择三个小组的概率为
种;(2)找出三名同学中至少有二人参加同一组活动的对立面,三名同学选择三个小组的概率为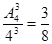 ,则可得所求概率为
,则可得所求概率为 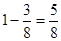 ;(3)X的可能取值为0,1,2,3,分别求出所对应的概率,列出分布列,进一步求出期望.
;(3)X的可能取值为0,1,2,3,分别求出所对应的概率,列出分布列,进一步求出期望.
解:(1)甲、乙、丙三名同学每人选择四个小组的方法是4种,故有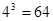 种.(4分)
种.(4分)
(2)甲、乙、丙三名同学选择三个小组的概率为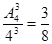 ,
,
所以三名同学至少有二人选择同一小组的概率为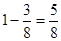 . (8分)
. (8分)
(3)由题意X的可能取值为:0,1,2,3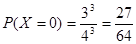 ,
,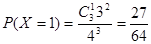 ,
,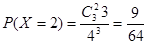 ,
,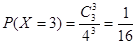 , (12分)
, (12分)
所以X的分布列如下:X 0 1 2 3 P 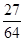
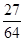
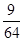
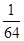
故数学期望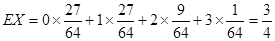 . (14分)
. (14分)
考点:1.排列组合;2.离散型随机变量的分布列与期望.

某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
| 赔付金额(元) | 0 | 1000 | 2000 | 3000 | 4000 |
| 车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(2)在样本车辆中,车主是新司机的占
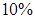 ,在赔付金额为4000元的样本车辆中,车主是新司机的占
,在赔付金额为4000元的样本车辆中,车主是新司机的占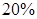 ,(3)估计在已投保车辆中,新司机获赔金额为4000元的概率.
,(3)估计在已投保车辆中,新司机获赔金额为4000元的概率. 计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量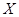 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量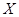 限制,并有如下关系:
限制,并有如下关系:
年入流量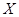 | 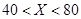 | 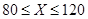 | 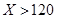 |
| 发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
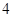 名男生和
名男生和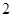 名女生中任选
名女生中任选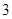 人参加演讲比赛,
人参加演讲比赛,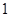 名女生的概率;
名女生的概率;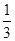 .
.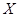 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求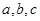 满足
满足 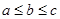 ,则称
,则称 为这三个数的中位数).
为这三个数的中位数).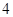 名男生和
名男生和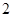 名女生中任选
名女生中任选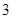 人参加演讲比赛,
人参加演讲比赛,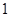 名女生的概率;
名女生的概率;