题目内容
从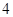 名男生和
名男生和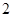 名女生中任选
名女生中任选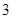 人参加演讲比赛,
人参加演讲比赛,
①求所选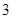 人都是男生的概率;
人都是男生的概率;
②求所选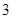 人恰有
人恰有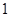 名女生的概率;
名女生的概率;
③求所选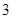 人中至少有
人中至少有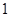 名女生的概率。
名女生的概率。
(1) ;(2)
;(2)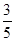 ;(3)
;(3) .
.
解析试题分析:(1)首先列出所有的情况,所有的选法共有20 种,其中,所选3人都是男生的选法有4种,由此求得所选3人都是男生的概率.(2)所选3人恰有1名女生的选法有12 种,所有的选法共有,由此可得所选3人恰有1名女生的概率.(3)方法一:用A表示所选3人均为男生,则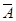 表示所选
表示所选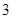 人中至少有
人中至少有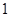 名女生,所以根据对立事件的和为1,即可求出答案; 方法二:用B表示恰有1名女生,用C表示两名女生均当选,则B+C表示所选
名女生,所以根据对立事件的和为1,即可求出答案; 方法二:用B表示恰有1名女生,用C表示两名女生均当选,则B+C表示所选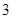 人中至少有
人中至少有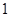 名女生,由于事件B与C互斥,且P(B)=
名女生,由于事件B与C互斥,且P(B)= 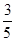 ,P(C)=
,P(C)= 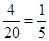
所以P(B+C)=P(B)+P(C)即可求出答案.
解:从4男2女中任选3人,用无序数对(x,y,z)表示如下:其中1,2,3,4为男,5,6为女
(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,3,4),(1,3,5),(1,3,6),(1,4,5),
(1,4,6),(1,5,6),(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6),(3,4,5),
(3,4,6),(3,5,6),(4,5,6)共20种结果,每种出现的可能性相同,故试验属古典概型。
(1)用A表示所选3人均为男生,则事件A包含的基本事件有4个,则P(A)= 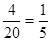 ;
;
(2)用B表示恰有1名女生,则事件B包含的基本事件有12个,则P(B)=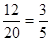 ;
;
(3)方法一:用A表示所选3人均为男生,则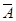 表示所选
表示所选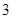 人中至少有
人中至少有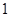 名女生,
名女生,
所以P(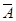 )=1-P(A)=1-
)=1-P(A)=1- =
= ;
;
方法二:用C表示两名女生均当选,则B+C表示所选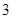 人中至少有
人中至少有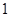 名女生,
名女生,
由于事件B与C互斥,且P(B)= 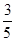 ,P(C)=
,P(C)= 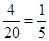
所以P(B+C)="P(B)+P(C)=" 
综上可知:(1)所选3人均为男生的概率为 ;
;
(2)所选3人中恰有1名女生的概率为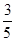
(3)所选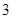 人中至少有
人中至少有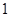 名女生的概率为
名女生的概率为
考点:古典概型及其概率计算公式.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:
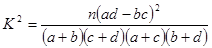 其中
其中
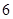 道备选题中一次性随机抽取
道备选题中一次性随机抽取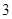 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中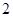 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成,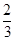 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.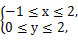 从区域W中随机取点M(x,y).
从区域W中随机取点M(x,y).