题目内容
11.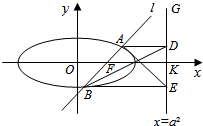 如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.(1)若抛物线x2=4$\sqrt{3}$y的焦点为椭圆的上顶点,求椭圆C的方程.
(2)若点N($\frac{{a}^{2}+1}{2}$,0)为x轴上一点,求证:$\overrightarrow{AN}$=λ$\overrightarrow{NE}$.
分析 (1)由题设条件知c=1,b=$\sqrt{3}$,a2=b2+c2=4,进而可得结论;
(2)当直线l的斜率为0或者不存在时,易知结论成立;当直线l的斜率存在且不为0时,通过设A(x1,y1),B(x2,y2),E(α2,y2),通过联立直线与椭圆方程,利用韦达定理计算kAN-kEN=0,即得结论.
解答 (1)解:∵直线l:x=my+1与x轴交点为(1,0),
∴椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F(1,0),
∴c=1,
∵抛物线x2=4$\sqrt{3}$y的焦点为(0,$\sqrt{3}$),
∴b=$\sqrt{3}$,
∴a2=b2+c2=3+1=4,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)证明:①当直线l的斜率为0或者不存在时,
显然点N($\frac{{α}^{2}+1}{2}$,0)为线段FK的中点,
此时显然成立;
②当直线l的斜率存在且不为0时,
设A(x1,y1),B(x2,y2),则E(α2,y2),
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,消去x整理得:
(a2+b2m2)y2+2mb2y+b2(1-a2)=0,
∴y1+y2=-$\frac{2m{b}^{2}}{{a}^{2}+{b}^{2}{m}^{2}}$,y1•y2=$\frac{{b}^{2}(1-{a}^{2})}{{a}^{2}+{b}^{2}{m}^{2}}$,
∴kAN-kEN=$\frac{{y}_{1}-0}{{x}_{1}-\frac{{α}^{2}+1}{2}}$-$\frac{{y}_{2}-0}{{α}^{2}-\frac{{α}^{2}+1}{2}}$
=$\frac{{y}_{1}}{m{y}_{1}+1-\frac{{α}^{2}+1}{2}}$-$\frac{{y}_{2}}{{α}^{2}-\frac{{α}^{2}+1}{2}}$
=$\frac{{y}_{1}}{m{y}_{1}+\frac{1-{α}^{2}}{2}}$-$\frac{{y}_{2}}{\frac{{α}^{2}-1}{2}}$
=$\frac{\frac{1-{α}^{2}}{2}•{(y}_{1}+{y}_{2})+m{y}_{1}•{y}_{2}}{\frac{1-{α}^{2}}{2}(m{y}_{1}+\frac{1-{α}^{2}}{2})}$
又∵$\frac{1-{α}^{2}}{2}$•(y1+y2)+my1•y2
=$\frac{1-{α}^{2}}{2}$•(-$\frac{2m{b}^{2}}{{a}^{2}+{b}^{2}{m}^{2}}$)+m•$\frac{{b}^{2}(1-{a}^{2})}{{a}^{2}+{b}^{2}{m}^{2}}$
=-$\frac{(1-{α}^{2})•m•{b}^{2}}{{a}^{2}+{b}^{2}{m}^{2}}$+$\frac{m{b}^{2}(1-{α}^{2})}{{a}^{2}+{b}^{2}{m}^{2}}$
=0,
∴kAN=kEN,即A、N、E三点共线,
故存在实数λ使得$\overrightarrow{AN}$=λ$\overrightarrow{NE}$.
点评 本题考查圆锥曲线和直线的位置关系和综合运用,解题时要认真审题,仔细解答,注意解题方法的积累,属于中档题.

| A. | 0.8874 | B. | 0.0026 | C. | 0.0013 | D. | 0.9987 |
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
| A. | {2} | B. | 2 | C. | {-3,-1,1,2,3} | D. | φ |
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$,$\overrightarrow{b}$都是单位向量,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=0,则$\overrightarrow{a}$=$\overrightarrow{b}$ | D. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}∥\overrightarrow{b}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ |