题目内容
1.椭圆C的中心在原点、焦点在x轴上,椭圆C的两个焦点及短轴的两个端点恰是一个面积为8的正方形的四个顶点.(1)求椭圆C的方程;
(2)设直线y=kx+b与椭圆C恒有两个横坐标不同的交点A、B,
①写出满足上述要求的充要条件(用含k、b的式子表示);
②若线段AB的垂直平分线与x轴交于点P(x0,0),求x0的取值范围.
分析 (1)通过题意可知b=c、a2=8,进而可得结论;
(2)①通过联立直线与椭圆方程,消去y整理得关于x的一元二次方程,只需根的判别式大于0,计算即可:
②通过垂直平分线的性质易知|PA|=|PB|,即(x1-x0)2+y12=(x2-x0)2+y22,利用点A、B在椭圆上及-$2\sqrt{2}$≤x1、x2≤$2\sqrt{2}$且x1≠x2,代入计算即可.
解答 解:(1)依题意,设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
焦距为2c,由题设条件知a2=8,b=c,
∴b2=$\frac{{b}^{2}+{c}^{2}}{2}$=$\frac{1}{2}$a2=4,
故椭圆C的方程式为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)①联立$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去y整理得:
(1+2k2)x2+4kbx+2b2-8=0,
∵直线y=kx+b与椭圆C恒有两个横坐标不同的交点A、B,
∴△=(4kb)2-4(1+2k2)(2b2-8)>0,
整理得:4+8k2>b2,
即直线y=kx+b与椭圆C恒有两个横坐标不同的交点的充要条件是4+8k2>b2;
②若线段AB的垂直平分线与x轴交于点P(x0,0),求x0的取值范围.
设A、B的坐标分别为(x1,y1)和(x2,y2).
∵线段AB的垂直平分线与x轴相交,
∴AB不平行于y轴,即x1≠x2.
又∵交点为P(x0,0),
∴|PA|=|PB|,即
(x1-x0)2+y12=(x2-x0)2+y22 (*)
∵A、B在椭圆上,
∴${{y}_{1}}^{2}$=4-$\frac{1}{2}$${{x}_{1}}^{2}$,${{y}_{2}}^{2}$=4-$\frac{1}{2}$${{x}_{2}}^{2}$,
代入(*)式得:2(x2-x1)x0=$\frac{1}{2}$(${{x}_{2}}^{2}$-${{x}_{1}}^{2}$),
∵x1≠x2,
∴x0=$\frac{1}{2}$•$\frac{{x}_{1}+{x}_{2}}{2}$,
∵-$2\sqrt{2}$≤x1、x2≤$2\sqrt{2}$,且x1≠x2,
∴-$4\sqrt{2}$<x1+x2<$4\sqrt{2}$,
∴-$\sqrt{2}$<x0<$\sqrt{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 我国对PM2.5采用如下标准:
我国对PM2.5采用如下标准:| PM2.5日均值m(微克/立方米) | 空气质量等级 |
| m<35 | 一级 |
| 35≤m≤75 | 二级 |
| m>75 | 超标 |
(Ⅰ)期间刘先生有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(Ⅱ)从所给15天的数据中任意抽取三天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列及期望.
| A. | [0,π] | B. | [0,$\sqrt{2}$π] | C. | [0,$\sqrt{3}π$] | D. | [0,2π] |
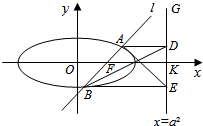 如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.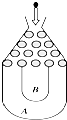 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是p,1-p.