题目内容
20.若关于x的不等式|2x-1|≥|1+a|-|2-a|对任意实数a恒成立,则x的取值范围是( )| A. | (-∞,0]∪[1,+∞) | B. | [0,1] | C. | (-∞,-1]∪[2,+∞) | D. | [-1,2] |
分析 由条件利用绝对值的意义求得|1+a|-|2-a|的最大值为3,可得|2x-1|≥3,由此求得x的取值范围.
解答 解:|1+a|-|2-a|表示数轴上的a对应点到-1 对应点的距离减去它到2对应点的距离,它的最大值为3,
∴|2x-1|≥3,∴2x-1≥3或2x-1≤-3,求得x≥2或 x≤-1,
故选:C.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
10.若动点A,B分别在直线l1:x+2y-1=0和l2:2x+4y+5=0上移动,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$|(O为原点)的最小值是( )
| A. | $\frac{3\sqrt{5}}{10}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{5}}{20}$ | D. | $\frac{7\sqrt{5}}{10}$ |
5.已知过抛物线C:x2=2py(p>0)的焦点F的直线m交抛物线于点M、N,|MF|=2|NF|=3,则抛物线C的方程为( )
| A. | x2=8y | B. | x2=2y | C. | x2=4y | D. | x2=2$\sqrt{2}$y |
12.用秦九韶算法计算多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6,当x=-4时,v4的值为( )
| A. | -57 | B. | 220 | C. | -845 | D. | 3392 |
9.如图所示的是“概率”知识的( )


| A. | 流程图 | B. | 结构图 | C. | 程序框图 | D. | 直方图 |
10.若钝角三角形ABC三内角A,B,C的度数成等差数列,且最大边长与最小边长的比为m,则m的取值范围是( )
| A. | 1<m≤2 | B. | 1<m<2 | C. | m>2 | D. | m≥2 |
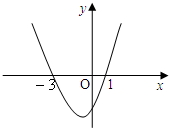 设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.
设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.