题目内容
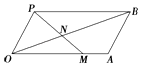
【题目】如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若 ![]() ,
, ![]() .
. 
(1)把y用x表示出来(即求y=f(x)的解析式);
(2)设数列{an}的首项a1=1,前n项和Sn满足Sn=f(Sn﹣1)(n≥2且n∈N*),求数列{an}的通项公式.
【答案】
(1)解:∵ ![]() ,
, ![]() ,
,
∴ ![]() =x,
=x, ![]() ,∴
,∴ ![]() ,
,
∵△OMN∽△BPN,
∴ ![]() ,
,
∴ ![]() ,
,
∴y=f(x)= ![]()
(2)解:Sn=f(Sn﹣1)= ![]() ,
,
∴ ![]() =
= ![]() ,∴
,∴ ![]() ﹣
﹣ ![]() =1,
=1,
∵S1=a1=1,∴数列{ ![]() }是首项为1,公差为1的等差数列,
}是首项为1,公差为1的等差数列,
∴ ![]() =n,即Sn=
=n,即Sn= ![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∴an= 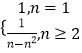
【解析】(1)利用 ![]() 得出方程得出f(x);(2)对Sn=f(Sn﹣1)=
得出方程得出f(x);(2)对Sn=f(Sn﹣1)= ![]() 取倒数,即可得出{
取倒数,即可得出{ ![]() }为等差数列,从而求出Sn , 再利用an=
}为等差数列,从而求出Sn , 再利用an= ![]() .
.
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.

 目标测试系列答案
目标测试系列答案【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,![]() .
.
(1)![]() 与
与![]() 是否有较强的线性相关性? 请计算相关系数
是否有较强的线性相关性? 请计算相关系数![]() (精确到
(精确到![]() )说明.
)说明.
(2)并求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到
都精确到![]() );
);
(3)用(2)中的线性回归模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,
,
①线性相关系数 ,通常情况下当
,通常情况下当![]() 大于0.8时,认为两
大于0.8时,认为两
个变量有很强的线性相关性.
②其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ;
;


