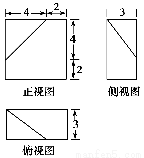
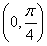题目内容
已知数列{an}中,a1=1,an+1= (n∈N*).
(n∈N*).
(1)求数列{an}的通项an;
(2)若数列{bn}满足bn=(3n-1) an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
(1)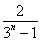 (2)-1<λ<2
(2)-1<λ<2
【解析】(1)由题知,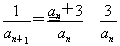 +1,
+1,
∴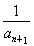 +
+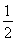 =3
=3 ,
,
∴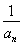 +
+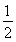 =
= ·3n-1=
·3n-1=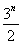 ,∴an=
,∴an=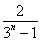 .
.
(2)由(1)知,bn=(3n-1)·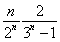 =n·
=n·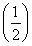 n-1,
n-1,
Tn=1×1+2×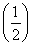 1+3×
1+3×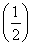 2+…+n·
2+…+n·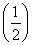 n-1,
n-1,
 Tn=1×
Tn=1×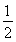 +2×
+2×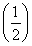 2+…+(n-1)
2+…+(n-1) 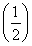 n-1+n
n-1+n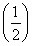 n,
n,
两式相减得,
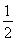 Tn=1+
Tn=1+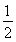 +
+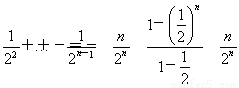 =2-
=2-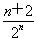 ,∴Tn=4-
,∴Tn=4-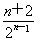 .
.
∵Tn+1-Tn=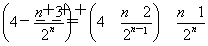 >0,
>0,
∴|Tn|为递增数列.
①当n为正奇数时,-λ<Tn对一切正奇数成立,
∵(Tn)min=T1=1,∴-λ<1,∴λ>-1;
②当n为正偶数时,λ<Tn对一切正偶数成立,
∵(Tn)min=T2=2,∴λ<2.
综合①②知,-1<λ<2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目