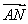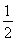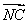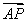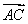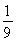题目内容
已知函数f(x)=2 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为 ,且点
,且点 是它的一个对称中心.
是它的一个对称中心.
(1)求f(x)的表达式;
(2)若f(ax)(a>0)在 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.
(1)2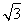 cos 2x.(2)
cos 2x.(2)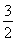
【解析】(1)由题意得f(x)的最小正周期为π,∴T=π=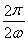 ,得ω=1.
,得ω=1.
∴f(x)=2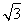 sin(2x+φ),
sin(2x+φ),
又点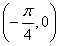 是它的一个对称中心,∴sin
是它的一个对称中心,∴sin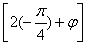 =0,得φ=
=0,得φ=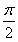 ,
,
∴f(x)=2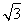 sin
sin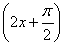 =2
=2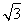 cos 2x.
cos 2x.
(2)由(1)得f(ax)=2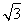 cos 2ax,∵2ax∈
cos 2ax,∵2ax∈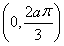 ,∴欲满足条件,必须
,∴欲满足条件,必须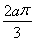 ≤π,
≤π,
∴a≤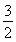 ,即a的最大值为
,即a的最大值为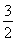 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目